题目内容
20.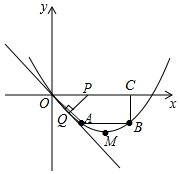 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,-2),B(6,-2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,-2),B(6,-2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=1时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围.
分析 (1)利用待定系数法即可解决问题;
(2)如图1中,当点O′与A重合时,点O′恰好在抛物线上.求出OP的长即可;
(3)分四种情形讨论即可①:如图2中,当0<t≤1时,重叠部分是△PQO′.②:如图3中,当1<t≤2时,重叠部分是四边形PQAH.③:如图4中,当2<t≤3时,重叠部分是△PEH.④:如图5中,当3<t<4时,重叠部分是△BEH.分别求解即可;
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,
把O(0,0),A(2,-2),B(6,-2)代入得:$\left\{\begin{array}{l}0=c\\ 4a+2b+c=-2\\ 36a+6b+c=-2\end{array}\right.$,
解得$\left\{\begin{array}{l}a=\frac{1}{6}\\ b=-\frac{4}{3}\\ c=0\end{array}\right.$,
所以抛物线的解析式为:$y=\frac{1}{6}{x^2}-\frac{4}{3}x$.
(2)如图1中,当点O′与A重合时,点O′恰好在抛物线上.
∵A(2,-2),
∴OA=2$\sqrt{2}$,OQ=$\sqrt{2}$,OP=2,
∴t=1时,点O′在抛物线上.
故答案为1.
(3)解:由题意A(2,-2),可知直线OA是第二四象限的角平分线,∠AOC=45°,PQ⊥OA,△OPQ与△O′PQ是全等的等腰直角三角形,OP=PO′=2t,PQ=$\sqrt{2}t$
①:如图2中,当0<t≤1时,重叠部分是△PQO′.
s=t2(0<t≤1)
②:如图3中,当1<t≤2时,重叠部分是四边形PQAH.
s=$\frac{1}{2}$•$\sqrt{2}$t•$\sqrt{2}$t-$\frac{1}{2}$(2t-2)2=-t2+4t-2(1<t≤2)
③:如图4中,当2<t≤3时,重叠部分是△PEH.
s=$\frac{1}{2}$•2•2=2.
④:如图5中,当3<t<4时,重叠部分是△BEH.
s=$\frac{1}{2}$•(8-2t)2.
综上所述,s=$\left\{\begin{array}{l}{{t}^{2}}&{(0<t≤1)}\\{-{t}^{2}+4t-2}&{(1<t≤2)}\\{2}&{(2<t≤3)}\\{\frac{1}{2}(8-2t)^{2}}&{(3<t<4)}\end{array}\right.$.
点评 本题考查二次函数综合题、待定系数法、翻折变换、等腰直角三角形的性质、多边形等面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建分段函数解决问题,属于中考压轴题.

 如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )
如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )| A. | 41° | B. | 49° | C. | 51° | D. | 59° |
| A. | a2•a3 | B. | (-a2)3 | C. | (a2)3 | D. | a12-a6 |

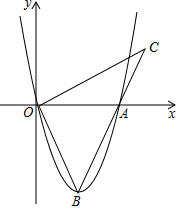 如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.
如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.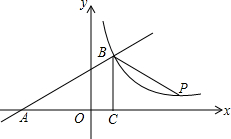 如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.
如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.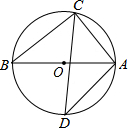 如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.
如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.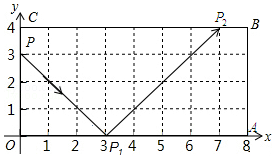 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4). 如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.