��Ŀ����
11���ڡ�ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E����1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ
����˵����ADC�ա�CEB�����ɣ�
����˵��DE=AD+BE�����ɣ�
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��DE=AD-BE
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��DE=BE-AD��

���� ��1��������֪�Ƴ���ADC=��BEC=90�㣬��Ϊ��ACD+��BCE=90�㣬��DAC+��ACD=90�㣬�Ƴ���DAC=��BCE������AAS���ɵõ��𰸣�
���ɢٵõ�AD=CE��CD=BE����������𰸣�
��2�����ۣ�DE=AD-BE���루1��֤�����ƿ�֤����ACD=��EBC�����Ƴ���ADC�ա�CEB���õ�AD=CE��CD=BE��������֪���ɵõ��𰸣�
��3�����ۣ�DE=BE-AD��֤���������ƣ�
��� �⣺��1����֤������ͼ1�У�
��AD��DE��BE��DE��
���ADC=��BEC=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬��DAC+��ACD=90�㣬
���DAC=��BCE��
�ڡ�ADC�͡�CEB�У�
$\left\{\begin{array}{l}{��CDA=��BEC}\\{��DAC=��ECB}\\{AC=BC}\end{array}\right.$��
���ADC�ա�CEB��AAS����
��֤�����ɣ�1��֪����ADC�ա�CEB��
��AD=CE��CD=BE��
��DC+CE=DE��
��AD+BE=DE��
��2�����ۣ�DE=AD-BE��
���ɣ���ͼ2�У���BE��EC��AD��CE��
���ADC=��BEC=90�㣬
���EBC+��ECB=90�㣬
�ߡ�ACB=90�㣬
���ECB+��ACE=90�㣬
���ACD=��EBC��
�ڡ�ADC�͡�CEB�У�
$\left\{\begin{array}{l}{��ACD=��CBE}\\{��ADC=��BEC}\\{AC=BC}\end{array}\right.$��
���ADC�ա�CEB��AAS����
��AD=CE��CD=BE��
��DE=EC-CD=AD-BE��
��3�����ۣ�DE=BE-AD��
�������£���ͼ3�У��ߡ�ACB=90�㣬
���ACD+��BCE=90��
��AD��MN��BE��MN��
���ADC=��CED=90�㣬
���ACD+��DAC=90�㣬
���DAC=��ECB��
�ڡ�ACD�͡�CBE�У�
$\left\{\begin{array}{l}{��ADC=��CEB}\\{��DAC=��ECB}\\{AC=CB}\end{array}\right.$��
���ACD�ա�CBE��AAS����
��AD=CE��CD=BE��
��DE=CD-CE=BE-AD��
�ʴ�ΪDE=AD-BE��DE=BE-AD��
���� ������Ҫ�������ڲ��ǵ����壬ȫ�������ε����ʺ��ж���֪ʶ�㣬�ܸ�����֪֤������ȫ�ȵ������ǽ����Ĺؼ������ͽϺã��ۺ��ԱȽ�ǿ��

 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�| A�� | 0 | B�� | 1 | C�� | -1 | D�� | -5 |
| A�� | x2-y2=��x-y��2 | B�� | a2+a+1=��a+1��2 | ||
| C�� | 2xy-6x=2x��y-3�� | D�� | a2+4a+21=a��a+4��+21 |
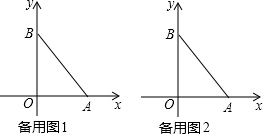
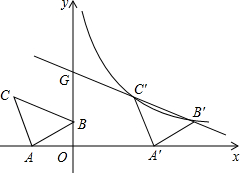 ��ͼ����ƽ��ֱ������ϵ����Rt��ABC����A=90�㣬AB=AC��A��-2��0����B��0��1����
��ͼ����ƽ��ֱ������ϵ����Rt��ABC����A=90�㣬AB=AC��A��-2��0����B��0��1����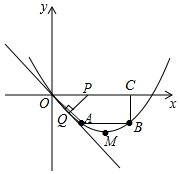 ��֪����ͼ�����ı���OABC�У�AB��OC��BC��x���ڵ�C��A��2��-2����B��6��-2��������P�ӵ�O����������x����������ÿ��2����λ���ٶ��ƶ�������P��PQ��ֱ��ֱ��OA������Ϊ��Q�����P�ƶ���ʱ��t�루0��t��4������OPQ���ı���OABC�ص����ֵ����ΪS��
��֪����ͼ�����ı���OABC�У�AB��OC��BC��x���ڵ�C��A��2��-2����B��6��-2��������P�ӵ�O����������x����������ÿ��2����λ���ٶ��ƶ�������P��PQ��ֱ��ֱ��OA������Ϊ��Q�����P�ƶ���ʱ��t�루0��t��4������OPQ���ı���OABC�ص����ֵ����ΪS��