题目内容
11.若实数x、y满足$y=\sqrt{2x-1}+\sqrt{1-2x}+\frac{1}{4}$,则$\frac{1}{2}xy$的平方根是$±\frac{1}{4}$.分析 根据二次根式有意义的条件可得2x-1≥0,1-2x≥0,再解可得x的值,进而可得y的值,然后再求$\frac{1}{2}xy$的平方根.
解答 解:由题意得:2x-1≥0,1-2x≥0,
解得:x=$\frac{1}{2}$,
则:y=$\frac{1}{4}$,
∵$\frac{1}{2}xy$=$\frac{1}{2}×\frac{1}{2}×\frac{1}{4}$=$\frac{1}{16}$,
∴$\frac{1}{2}xy$的平方根是±$\frac{1}{4}$,
故答案为:$±\frac{1}{4}$.
点评 此题主要考查了二次根式有意义的条件,关键是掌握被开方数必须是非负数.

练习册系列答案
相关题目
1.如果一个直角三角形的两条边分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值为( )
| A. | 5 | B. | $2\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 5或2$\sqrt{7}$ |
3.若实数x、y满足$\sqrt{2x-1}+$(y-1)2=0,则x+y的值等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
20.下列各式中,正确的是( )
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{4}$=2 | C. | $\root{3}{-64}$=-4 | D. | $\sqrt{{{{(-2)}^2}}}$=-2 |
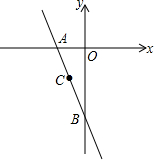 如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B
如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B 已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.
已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.