题目内容
2.解下列方程:(1)$\frac{2}{x-3}$=$\frac{3}{2x-1}$
(2)$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)方程两边同乘(x-3)(2x-1)得:2(2x-1)=3(x-3),
解得:x=-7,
检验:当x=-7时(x-3)(2x-1)=(-7-3)×(-14-1)=150≠0,
则x=-7是原方程的根;
(2)方程两边同乘(x-2)得:1=x-1-3(x-2),
解得:x=2,
检验:当x=2时 x-2=0
则x=2是增根,原方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
17.计算:22014-(-2)2015的结果是( )
| A. | 24029 | B. | 3×22014 | C. | -22014 | D. | ($\frac{1}{2}$)2014 |
7.点(-1,-1)关于原点对称的点的坐标是( )
| A. | (-1,1) | B. | (1,1) | C. | (1,-1) | D. | (0,0) |
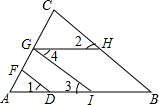 已知:如图,∠1=∠2,∠3=∠4,试说明DF∥BC.
已知:如图,∠1=∠2,∠3=∠4,试说明DF∥BC. 如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).
如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).