题目内容
16.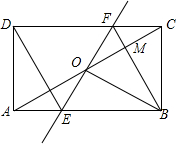 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①利用线段垂直平分线的性质的逆定理可得结论;
②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;
③可证明∠CDE=∠DFE;
④可通过面积转化进行解答.
解答 解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠CBF=30°,∠BEO=60°,
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∴S△AOE:S△BCM=2S△CMF:S△BCM=$\frac{2FM}{BM}$,
∵∠FCO=30°,
∴FM=$\frac{CM}{\sqrt{3}}$,BM=$\sqrt{3}$CM,
∴$\frac{FM}{BM}$=$\frac{1}{3}$,
∴S△AOE:S△BCM=2:3,
故④错误;
所以其中正确结论的个数为2个;
故选C.
点评 本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.

练习册系列答案
相关题目
4.以下列三个正数为三边长度能构成直角三角形的是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
11.下列各式中,计算过程正确的是( )
| A. | $\sqrt{{2^2}+{7^2}}$=2+7 | B. | $\sqrt{9\frac{1}{2}}$=3$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\frac{{\sqrt{8}+\sqrt{12}}}{{\sqrt{2}}}$=4+6 |
5.如果$\sqrt{3+a}$+(5-b)2=0,那么点A(a,b)关于原点对称的点A′的坐标为( )
| A. | (3,5) | B. | (3,-5) | C. | (-3,5) | D. | (5,-3) |
 如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4=18.
如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4=18.