题目内容
1. 如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4=18.
如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4=18.
分析 过F作AM的垂线交AM于N,通过证明S1+S2+S3+S4=Rt△ABC的面积×3,依此即可求解.
解答  解:过F作AM的垂线交AM于N,
解:过F作AM的垂线交AM于N,
则Rt△ANF≌Rt△ABC,Rt△NFK≌Rt△CAT,
所以S2=SRt△ABC.
由Rt△NFK≌Rt△CAT可得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
可得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
∵Rt△ABC≌Rt△EBD,
∴S4=SRt△ABC
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=SRt△ABC+SRt△ABC+SRt△ABC
=SRt△ABC×3
=4×3÷2×3
=18.
故答案为:18.
点评 本题考查勾股定理的知识,有一定难度,解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.下列变形,属于因式分解的有( )
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.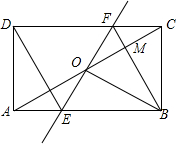 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13. 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )| A. | 124° | B. | 114° | C. | 104° | D. | 66° |
11.某校八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,其中说法错误的是( )
| A. | 这种调查方式是抽样调查 | |
| B. | 每名学生的立定跳远成绩是个体 | |
| C. | 100名学生是样本容量 | |
| D. | 这100名学生的立定跳远成绩是总体的一个样本 |
 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=68°,求∠ACB的度数.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=68°,求∠ACB的度数.