题目内容
7.一个直角三角形的两条直角边长分别为2a+1和3a-1,该三角形面积为S,试用含a的代数式表示S(结果要化成最简形式),并求当a=2时,S的值.分析 利用三角形面积公式表示出S,将a的值代入计算即可求出值.
解答 解:根据题意得:S=$\frac{1}{2}$(2a+1)(3a-1)=3a2+$\frac{1}{2}$a-$\frac{1}{2}$,
当a=2时,S=12+1-$\frac{1}{2}$=$\frac{25}{2}$.
点评 此题考查了多项式乘多项式,以及代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.下列各式中不能用平方差公式计算的是( )
| A. | (2x+y)(2x-y) | B. | (x-y)(y-x) | C. | (-x+y)(-x-y) | D. | (x+y)(-x+y) |
2.下列各式计算正确的是( )
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | 5$\sqrt{6}$-3$\sqrt{3}$=2$\sqrt{3}$ | C. | ($\sqrt{8}$+$\sqrt{50}$)÷2=$\sqrt{4}$+$\sqrt{25}$=7 | D. | 3$\sqrt{3}$+$\sqrt{27}$=6$\sqrt{3}$ |
12.下列变形,属于因式分解的有( )
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.若(x+2)(2x-n)=2x2+mx-2,则( )
| A. | m=3,n=1 | B. | m=5,n=1 | C. | m=3,n=-1 | D. | m=5,n=-1 |
16.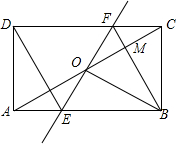 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
17.下列长度的三条线段能组成锐角三角形的是( )
| A. | 2,3,3 | B. | 2,3,4 | C. | 2,3,5 | D. | 3,4,5 |
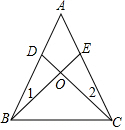 如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证:
如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证: