题目内容

4．以下列三个正数为三边长度能构成直角三角形的是（　　）
A．1，2，3B．2，3，4C．3，4，5D．4，5，6

分析 根据勾股定理的逆定理可知，当三角形中三边的关系为：a2+b2=c2时，则三角形为直角三角形．

解答 解：A、12+22≠32，不符合勾股定理的逆定理，不能组成直角三角形，故选项错误；
B、22+32≠42，不符合勾股定理的逆定理，不能组成直角三角形，故选项错误；
C、52+122=132，符合勾股定理的逆定理，能组成直角三角形，故选项正确；
D、42+52≠62，不符合勾股定理的逆定理，不能组成直角三角形，故选项错误．
故选C．

点评 此题考查的知识点是定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足：a2+b2=c2时，则三角形ABC是直角三角形．解答时，只需看两较小数的平方和是否等于最大数的平方．

练习册系列答案
相关题目
14．下列变形中，正确的是（　　）
A．由5x=-4得x=-$\frac{5}{4}$B．由4x+2=3x-1得4x+3x=2-1
C．由$\frac{x}{5}$-1=2得x-5=2D．由4x-3=2x-2得2x=1
15．下列各式中不能用平方差公式计算的是（　　）
A．（2x+y）（2x-y）B．（x-y）（y-x）C．（-x+y）（-x-y）D．（x+y）（-x+y）
12．下列变形，属于因式分解的有（　　）
①x2-16=（x+4）（x-4）②x2+3x-16=x（x+3）-16
③（x+4）（x-4）=x2-16　④x2+x=x（x+1）
A．1个B．2个C．3个D．4个
19．若（x+2）（2x-n）=2x2+mx-2，则（　　）
A．m=3，n=1B．m=5，n=1C．m=3，n=-1D．m=5，n=-1
9．如图1，在四边形ABCD中，AD∥BC，∠B=∠C=60°，P、Q同时从B出发，以每秒1单位长度分别沿B-A-D-C和B-C-D方向运动至相遇时停止，设运动时间为t（秒），△BPQ的面积为S（平方单位），S与t的函数图象如图2所示，则下列结论错误的个数（　　）                      
①当t=4秒时，S=4$\sqrt{3}$        ②AD=4    
③当4≤t≤8时，S=2$\sqrt{3}$t       ④当t=9秒时，BP平分四边形ABCD的面积．
A．1个B．2个C．3个D．4个
16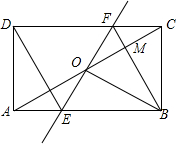．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=3：2．其中正确结论的个数是（　　）
A．4个B．3个C．2个D．1个
13．如图，将?ABCD沿对角线AC折叠，使点B落在点B'处．若∠1=∠2=44°，则∠B为（　　）
A．124°B．114°C．104°D．66°
14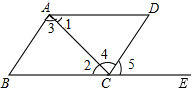．如图，四边形ABCD中，点E在BC延长线上，则下列条件中不能判断AB∥CD的是（　　）
A．∠3=∠4B．∠1=∠2C．∠5=∠ABCD．∠1+∠3+∠D=180°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网