题目内容
16.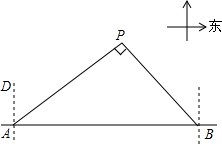 钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.(参考数据sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75,$\sqrt{2}$≈1.4)
(1)求P到A,B两船所在直线(即:直线AB)的距离;
(2)若执法船A,B分别以40海里/时,30海里/时的速度同时出发,匀速直线前进,试通过计算判断哪艘船先到达P处.
分析 (1)作PC⊥AB于点C,由题意得:∠PAC=36.5°,∠PBC=45°,设PC的长为x海里,分别在Rt△ACP中,和在Rt△BCP中,用x表示出AC和BC,然后根据AC+BC=140海里列出方程,解方程即可;
(2)先解Rt△ACP,求出AP,解Rt△BCP,求出BP,再分别求出甲、乙两船到达P处的时间,比较即可确定答案.
解答 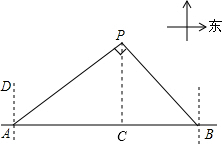 解:(1)如图,作PC⊥AB于点C,
解:(1)如图,作PC⊥AB于点C,
由题意得:∠PAC=90°-53.5°=36.5°,∠PBC=90°-45°=45°,
设PC的长为x海里.
∵在Rt△ACP中,tan∠PAC=$\frac{PC}{AC}$,
∴AC=$\frac{PC}{tan∠PAC}$≈$\frac{x}{0.75}$=$\frac{4}{3}$x;
∵在Rt△BCP中,tan∠PBC=$\frac{PC}{BC}$,
∴BC=$\frac{PC}{tan∠PBC}$=$\frac{x}{1}$=x;
∵AC+BC=AB,
∴$\frac{4}{3}$x+x=140,
∴x=60.
故P到A,B两船所在直线(即:直线AB)的距离为60海里;
(2)∵在Rt△ACP中,sin∠PAC=$\frac{PC}{AP}$,
∴AP=$\frac{PC}{sin∠PAC}$≈$\frac{30}{0.6}$=50,
∵在Rt△BCP中,sin∠PBC=$\frac{PC}{BP}$,
∴BP=$\frac{PC}{sin∠PBC}$=$\frac{30}{\frac{\sqrt{2}}{2}}$=30$\sqrt{2}$≈42,
∵执法船A,B分别以40海里/时,30海里/时的速度同时出发,匀速直线前进,
∴甲船到达P处所用时间为:50÷40=1.25(小时),
乙船到达P处所用时间为:42÷30=1.4(小时),
∵1.25<1.4,
∴甲船先到达P处.
点评 本题考查了解直角三角形的应用-方向角问题,解决本题的关键在于准确作出辅助线构造直角三角形,进而利用三角函数定义求解.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
 如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
如图,三条直线交于同一点,则∠1+∠2+∠3=180°. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.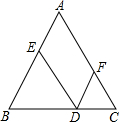 如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.
如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.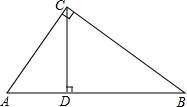 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )