题目内容
5.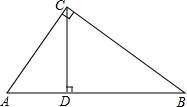 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )①AC•BC=AB•CD;②AC2-AD2=BC2-BD2;③CD2=AD•BD;④$\frac{1}{{A{C^2}}}+\frac{1}{{B{C^2}}}=\frac{1}{{A{B^2}}}$.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 如图,由三角形的面积公式证明AC•BC=AB•CD成立,得到①成立;由勾股定理、射影定理分别证明AC2-AD2=BC2-BD2、CD2=AD•BD成立,得到②③成立,即可解决问题.
解答  解:如图,∵△ABC为直角三角形,且CD⊥AB,
解:如图,∵△ABC为直角三角形,且CD⊥AB,
∴$\frac{1}{2}AC•BC=\frac{1}{2}AB•CD$,即AC•BC=AB•CD.
故选项①正确;由勾股定理得:
AC2-AD2=CD2,BC2-BD2=CD2,
∴AC2-AD2=BC2-BD2,
故选项②正确;由射影定理得:
CD2=AD•BD,故选项③正确,
综上所述,正确选项有三个.
故选B.
点评 该题主要考查了直角三角形中的射影定理、勾股定理及其应用问题;牢固掌握射影定理、勾股定理等几何知识点是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
9.如对于任意的实数a、b都有f(a+b)=f(a)+f(b)且f(1)=2,则$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(2)}$+$\frac{f(6)}{f(3)}$+…+$\frac{f(2012)}{f(1006)}$的值是( )
| A. | 1005 | B. | 1006 | C. | 2012 | D. | 2010 |
15.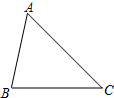 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )| A. | $\sqrt{2}$+$\sqrt{7}$ | B. | 3$\sqrt{2}$-$\sqrt{7}$ | C. | 3$\sqrt{2}$+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |
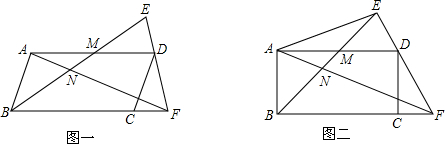
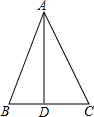 如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=2,AD=6,求CD的长,小明同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小明的思路,探究并解答下列问题:
如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=2,AD=6,求CD的长,小明同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小明的思路,探究并解答下列问题: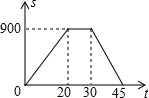 乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.
乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.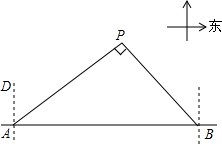 钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
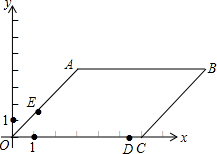 如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)