题目内容
11.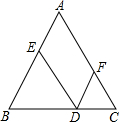 如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.
如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.
分析 根据DE∥AC,DF∥AB,所以四边形AEDF为平行四边形,所以AE=DF=3cm,DE=AF=5cm,再证明△BED为等边三角形,△DFC为等边三角形,得到E=BD=DE=5cm,DF=FC=CD=3cm,所以AB=AE+BE=8cm,AC=AF+CF=8cm,BC=BD+CD=8cm,即可解答.
解答 解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,
∴AE=DF=3cm,DE=AF=5cm,
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥AC,DF∥AB,
∴∠BED=∠A=60°,∠DFC=∠A=60°,
∴∠BED=∠B=60°,∠DFC=∠C=60°,
∴△BED为等边三角形,△DFC为等边三角形,
∴BE=BD=DE=5cm,DF=FC=CD=3cm,
∴AB=AE+BE=8cm,AC=AF+CF=8cm,BC=BD+CD=8cm,
∴△ABC的周长为:AB+AC+BC=8+8+8=24cm.
故答案为:24.
点评 本题考查了等边三角形的性质与判定,解决本题的关键是平行四边形和等边三角形的判定.

练习册系列答案
相关题目
1.下列各式中,正确的是( )
| A. | $\frac{6-2x}{-x+3}$=2 | B. | $\frac{a-b}{(a-b)(a+b)}$=0 | C. | $\frac{(a-b)^{3}}{(b-a)^{3}}$=1 | D. | $\frac{(a-b)^{2}}{(b-a)^{2}}$=-1 |

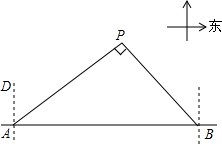 钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.