题目内容
11．
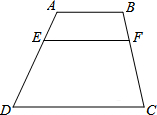如图，AB∥EF∥CD，AB=3，CD=7，AE：ED=1：3，则EF的长度为4．
分析 过点A作AM∥BC，交EF于点M，交CD于点N．由平行线分线段成比例定理得出比例式即可求解．
解答 解：过点A作AM∥BC，交EF于点M，交CD于点N．如图所示：
则NC=MF=AB=3．DN=CD-CN=7-3=4．
∵EF∥CD，
∴$\frac{EM}{DN}=\frac{AE}{AD}$=$\frac{1}{4}$，
∴EM=$\frac{1}{4}$DN=1．
∴EF=EM+MF=1+3=4；
故答案为：4．
点评 本题主要考查了平行线分线段成比例定理，可以通过作平行线转化为三角形的问题解决．
练习册系列答案
阅读快车系列答案
相关题目
已知依次函数y=x+1．
19．以下列长度的线段为边能构成直角三角形的是（ ）
| A． | 1，2，3 | B． | 6，8，12 | C． | 5，12，5 | D． | 7，24，25 |
16．
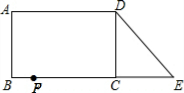已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为t秒，当t的值为（ ）秒时．△ABP和△DCE全等．
已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为t秒，当t的值为（ ）秒时．△ABP和△DCE全等．| A． | 1 | B． | 1或3 | C． | 1或7 | D． | 3或7 |
20．
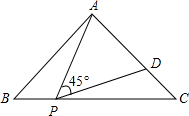如图，等腰直角△ABC的直角边长为3，P为斜边BC上的一点，且BP=1，D为AC上一点，若∠APD=45度，则以PA为边的正方形的面积为（ ）
如图，等腰直角△ABC的直角边长为3，P为斜边BC上的一点，且BP=1，D为AC上一点，若∠APD=45度，则以PA为边的正方形的面积为（ ）| A． | 10-3$\sqrt{2}$ | B． | 10-2$\sqrt{3}$ | C． | 4 | D． | 6 |