题目内容
16．请写出一个一次函数的表达式，它的图象过点（0，-2），且y的值随x值增大而减小，这表达式为：y=-x-2．分析 设一次函数解析式为y=kx+b，根据一次函数的性质，k可取-1，然后把（0，-2）代入y=-x+b求出b的值即可得到一个满足条件的一次函数解析式．
解答 解：设一次函数解析式为y=kx+b，
∵函数值y随自变量x的增大而减小的，
∴k可取-1，
把（0，-2）代入y=-x+b得b=-2，
∴一次函数解析式为y=-x-2．
故答案为y=-x-2．
点评 本题考查了一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．由于y=kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．
练习册系列答案
名校课堂系列答案
相关题目
7．老师组织学生做分组摸球实验．给每组准备了完全相同的实验材料，一个不透明的袋子，袋子中装有除颜色外都相同的4个黄球和若干个白球．先把袋子中的球搅匀后，从中随意摸出一个球，记下球的颜色再放回，统计各组实验的结果如下：
请你估计袋子中白球的个数是1．
| 一组 | 二组 | 三组 | 四组 | 五组 | 六组 | 七组 | 八组 | 九组 | 十组 | |
| 摸球的次数 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 摸到白球的次数 | 21 | 16 | 20 | 23 | 19 | 18 | 25 | 20 | 22 | 18 |
4．数轴上，在原点的两旁且与原点距离相等的两点所表示的数是（ ）
| A． | 互为倒数 | B． | 互为相反数 | C． | 相等 | D． | 不能判定 |
1．已知二次函数y=x2-bx-1（b＞1），则下列说法正确的是（ ）
| A． | 无法判断其图象与x轴是否有交点 | |
| B． | 其对称轴与x轴交于负半轴 | |
| C． | 若点（m，n）在y=x2-bx-1的图象上，则n≥-1 | |
| D． | 若点（-3，y1）、（2，y2）都在y=x2-bx-1的图象上，则y1＞y2 |
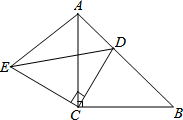如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：
6．
如图，△ABC≌△DEF，则∠C的度数是（ ）
如图，△ABC≌△DEF，则∠C的度数是（ ）| A． | 56° | B． | 51° | C． | 107° | D． | 73° |