题目内容
13. 如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,则MD的长为5.
如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,则MD的长为5.
分析 延长BD交AC于N,根据等腰三角形三线合一得到BD=DN,AN=AB,根据三角形中位线定理得到DM=$\frac{1}{2}$NC,代入计算即可.
解答  解:延长BD交AC于N,
解:延长BD交AC于N,
∵AD是∠BAC的平分线,BD⊥AD,
∴BD=DN,AN=AB=12,
∵BM=CM,BD=DN,AC=22,
∴DM=$\frac{1}{2}$NC=$\frac{1}{2}$(AC-AN)=5,
则MD的长为5.
点评 本题考查的是三角形中位线定理和等腰三角形的性质的应用,掌握三角形的中位线平行于第三边且等于第三边的一半和等腰三角形三线合一是解题的关键.

练习册系列答案
相关题目
3.下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
| A. | a=1.5,b=2,c=3 | B. | a=3,b=4,c=5 | C. | a=6,b=8,c=10 | D. | a=7,b=24,c=25 |
1.下列是二次根式的是( )
| A. | $\root{3}{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^{2}}$ | D. | $\sqrt{a}$ |
8.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用了这两种货车的情况如表所示;现用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货.
(1)问甲、乙两种货车每辆一次分别可运货多少吨?
(2)如果按每吨付费30元计算,货主应付运费多少元?
| 第一次 | 第二次 | |
| 甲种货车辆数(单位;辆) | 2 | 5 |
| 乙种货车辆数(单位:辆) | 3 | 6 |
| 累计运货吨数(单位:吨) | 15.5 | 35 |
(2)如果按每吨付费30元计算,货主应付运费多少元?
18.某学校号召同学们为灾区学生自愿捐款.已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等.如果设第一次捐款人数为x人,那么x满足的方程是( )
| A. | $\frac{4800}{x}=\frac{5000}{x-20}$ | B. | $\frac{4800}{x}=\frac{5000}{x+20}$ | C. | $\frac{4800}{x-20}=\frac{5000}{x}$ | D. | $\frac{4800}{x+20}=\frac{5000}{x}$ |
5. 如图,图中的同位角的对数是( )
如图,图中的同位角的对数是( )
 如图,图中的同位角的对数是( )
如图,图中的同位角的对数是( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
3.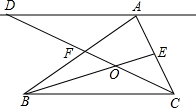 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |