题目内容
12.已知二次函数y=a(x-h)2+k的图象经过(0,5),(10,8)两点,若a<0,0<h<10,则h的值可能是( )| A. | 7 | B. | 5 | C. | 3 | D. | 1 |
分析 根据二次函数的对称性确定出对称轴的范围,然后求解即可.
解答 解:∵a<0,
∴抛物线开口向下,
∵图象经过(0,5)、(10,8)两点,0<h<10,
∴对称轴在5到10之间,
∴h的值可能是7.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,从二次函数的对称性考虑求解是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
3.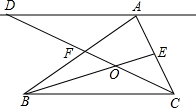 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
20.某商品的标价为400元,8折销售仍赚120元,则商品进价为( )
| A. | 150元 | B. | 200元 | C. | 300元 | D. | 440元 |
7.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法不正确的是( )
| A. | 方程x2-4x+3=0是3倍根方程 | |
| B. | 若关于x的方程(x-3)(mx+n)=0是3倍根方程,则m+n=0 | |
| C. | 若m+n=0且m≠0,则关于x的方程(x-3)(mx+n)=0是3倍根方程 | |
| D. | 若3m+n=0且m≠0,则关于x的方程x2+(m-n)x-mn=0是3倍根方程 |
2.皖星书店年初以每本20元的价格购进一批畅销书《莫言精品集》,销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如表所示,按照表中y与x的关系规律,解决下面的问题:
(1)试求出y与x的函数关系式.
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
| x | 25 | 28 | 30 | 32 | 35 |
| y | 250 | 220 | 200 | 180 | 150 |
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
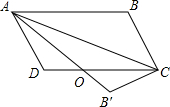 如图,在平行四边形ABCD中将△ABC沿AC对折,使点B落在B′处,AB′和CD相交于O,求证:OD=OB′.
如图,在平行四边形ABCD中将△ABC沿AC对折,使点B落在B′处,AB′和CD相交于O,求证:OD=OB′.