题目内容
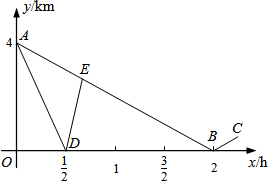 【实际情境】
【实际情境】某中学九年级学生步行到郊外春游.一班的学生组成前队,速度为4km/h,二班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时,后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
【数学研究】
若不计队伍的长度,如图,折线A-B-C、A-D-E分别表示后队、联络员在行进过程中,离前队的路程y(km)与后队行进时间x(h)之间的部分函数图象.
(1)求线段AB对应的函数关系式;
(2)求点E的坐标,并说明它的实际意义;
(3)联络员从出发到他折返后第一次与后队相遇的过程中,当x为何值时,他离前队的路程与他离后队的路程相等?
考点:一次函数的应用
专题:
分析:(1)设线段AB对应的函数关系式为y1=kx+b.由待定系数求出其解即可;
(2)根据路程=速度×时间就可以表示出DE的解析式,再求出y2与y1的交点坐标就是点E的坐标;
(3)设AD的关系式为y3=k3x+b3,求出解析式,再分两种情况建立建立方程求出其解即可.
(2)根据路程=速度×时间就可以表示出DE的解析式,再求出y2与y1的交点坐标就是点E的坐标;
(3)设AD的关系式为y3=k3x+b3,求出解析式,再分两种情况建立建立方程求出其解即可.
解答:解:(1)设线段AB对应的函数关系式为y1=kx+b.根据题意,得
,
解得
.
∴y1=-2x+4;
(2)根据题意,得线段DE对应的函数关系式为
y2=(12+4)(x-
)=16x-8.(3分)
当y1=y2时,-2x+4=16x-8,解得x=
.(4分)
把x=
代入y1=-2x+4中,得y1=
,即点E的坐标为(
,
).
点E的实际意义为联络员出发
h后与后队相遇,此时他与前队的距离为
km;
(3)根据题意,得线段AD对应的函数关系式为y3=k3x+b3,由题意,得
,
解得:
∴y3=-8x+4.
分两种情况:
①y1=2y3,即-2x+4=2(-8x+4),解得x=
.
②y1=2y2,即-2x+4=2(16x-8),解得x=
.
综上,联络员从出发到他折返后第一次与后队相遇的过程中,当x为
或
时,他离前队的路程与他离后队的路程相等.
|
解得
|
∴y1=-2x+4;
(2)根据题意,得线段DE对应的函数关系式为
y2=(12+4)(x-
| 1 |
| 2 |
当y1=y2时,-2x+4=16x-8,解得x=
| 2 |
| 3 |
把x=
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
点E的实际意义为联络员出发
| 2 |
| 3 |
| 8 |
| 3 |
(3)根据题意,得线段AD对应的函数关系式为y3=k3x+b3,由题意,得
|
解得:
|
∴y3=-8x+4.
分两种情况:
①y1=2y3,即-2x+4=2(-8x+4),解得x=
| 2 |
| 7 |
②y1=2y2,即-2x+4=2(16x-8),解得x=
| 10 |
| 17 |
综上,联络员从出发到他折返后第一次与后队相遇的过程中,当x为
| 2 |
| 7 |
| 10 |
| 17 |
点评:本题考查了运用待定系数法求一次函数的解析式的运用,一次函数与二元一次方程组的关系的运用,一元一次方程的解法的运用,解答时求出一次函数的关系式是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 观察函数y1和y2的图象,当x=0,两个函数值的大小为( )
观察函数y1和y2的图象,当x=0,两个函数值的大小为( )| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1≥y2 |
 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2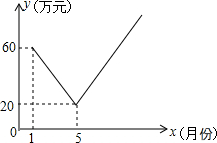 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图. 已知,如图,点B、E、F、C在同一条直线上,∠A=∠D,BE=CF,∠B=∠C.
已知,如图,点B、E、F、C在同一条直线上,∠A=∠D,BE=CF,∠B=∠C.