题目内容
 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2| 3 |
(1)直接写出∠ACO的度数;
(2)求证:OC=BC;
(3)求直线CD对应的函数表达式.
考点:圆的综合题
专题:
分析:(1)直接根据等边三角形的性质及圆周角定理即可得出结论;
(2)根据直角三角形的性质得出∠CAO=∠CAB=30°,再由等边三角形三线合一的性质得出AC是OB的垂直平分线,根据垂径定理即可得出结论;
(3)根据圆周角定理得出AC是直径,由CD是圆的切线得出CD⊥AC.再根据∠ACO=∠B=60°可知∠DCO=∠CAO=30°.故可得出OC,OD的长,进而得出C、D两点的坐标,利用待定系数法求出直线CD对应的函数表达式即可.
(2)根据直角三角形的性质得出∠CAO=∠CAB=30°,再由等边三角形三线合一的性质得出AC是OB的垂直平分线,根据垂径定理即可得出结论;
(3)根据圆周角定理得出AC是直径,由CD是圆的切线得出CD⊥AC.再根据∠ACO=∠B=60°可知∠DCO=∠CAO=30°.故可得出OC,OD的长,进而得出C、D两点的坐标,利用待定系数法求出直线CD对应的函数表达式即可.
解答:(1)解:∵△OAB是等边三角形,
∴∠ACO=∠ABO=60°;
(2)证明:∵∠AOC=90°,∠ACO=60°,∠OAB=60°,
∴∠CAO=∠CAB=30°.
∴AC是OB的垂直平分线,
∴OC=BC;
(3)解:∵∠AOC=90°,
∴AC是直径.
∵CD是圆的切线,
∴CD⊥AC.
又∵∠ACO=∠B=60°,
∴∠DCO=∠CAO=30°.
∴OC=2,OD=
.
∴C(0,2),D(-
,0).
设直线CD对应的函数表达式为y=kx+b(b≠0),
∴
,
∴
,
∴直线CD对应的函数表达式为y=
x+2.
∴∠ACO=∠ABO=60°;
(2)证明:∵∠AOC=90°,∠ACO=60°,∠OAB=60°,
∴∠CAO=∠CAB=30°.
∴AC是OB的垂直平分线,
∴OC=BC;
(3)解:∵∠AOC=90°,
∴AC是直径.
∵CD是圆的切线,
∴CD⊥AC.
又∵∠ACO=∠B=60°,
∴∠DCO=∠CAO=30°.
∴OC=2,OD=
2
| ||
| 3 |
∴C(0,2),D(-
2
| ||
| 3 |
设直线CD对应的函数表达式为y=kx+b(b≠0),
∴
|
∴
|
∴直线CD对应的函数表达式为y=
| 3 |
点评:本题考查的是圆的综合题,涉及到圆周角定理、垂径定理、切线的性质及等边三角形的性质等知识,难度适中.

练习册系列答案
相关题目
(-2xy)3的计算结果( )
| A、-2x3y3 |
| B、-8x3y3 |
| C、8x4y4 |
| D、8xy4 |
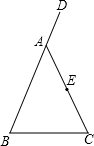 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.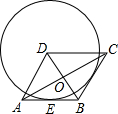 如图,在菱形ABCD中,AB=2
如图,在菱形ABCD中,AB=2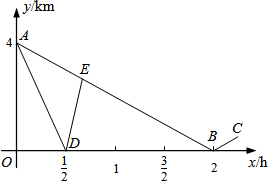 【实际情境】
【实际情境】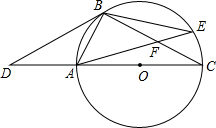 如图,D是⊙O直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,D是⊙O直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.