题目内容
已知，如图，点B、E、F、C在同一条直线上，∠A=∠D，BE=CF，∠B=∠C．求证：AF=DE．
考点：全等三角形的判定与性质
专题：证明题
分析：根据等式的性质，可得BF与CE的关系，根据AAS，可得三角形全等，根据全等三角形的性质，可得对应边相等．
解答：证明：∵BE=CF，
∴BE+EF=CF+F，即BF=CE．
在△ABF和△DCE中，
∵
，
∴△ABF≌△DCE（AAS），
∴AF=DE（全等三角形对应边相等）．
∴BE+EF=CF+F，即BF=CE．
在△ABF和△DCE中，
∵
|
∴△ABF≌△DCE（AAS），
∴AF=DE（全等三角形对应边相等）．
点评：本题考查了全等三角形的判定与性质，AAS证明三角形全等，全等三角形的性质证明结论．
练习册系列答案
相关题目
【实际情境】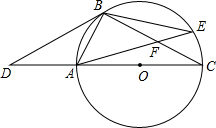
如图，D是⊙O直径CA延长线上一点，点B在⊙O上，且AB=AD=AO．