题目内容
18. 如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
分析 (1)由平行四边形的性质得出AD=BC,∠ABC+∠BAD=180°,由等腰三角形的性质得出∠ABC=∠ACB.证出∠BAD=∠ACE,CE=AD,由SAS证明△ADB≌△CEA即可;
(2)由全等三角形的性质得出AE=BD=6,由平行线得出△ADF∽△EBF,得出对应边成比例,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ABC+∠BAD=180°.
又∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB+∠ACE=180°,
∴∠BAD=∠ACE.
∵CE=BC,
∴CE=AD,
在△ABE和△CEA中,$\left\{\begin{array}{l}{CE=AD}&{\;}\\{∠BAD=∠ACE}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△ADB≌△CEA(SAS).
(2)解:∵△ADB≌△CEA,
∴AE=BD=9.
∵AD∥BC,
∴△ADF∽△EBF.
∴$\frac{AF}{EF}=\frac{AD}{BE}$=$\frac{1}{2}$.
∴$\frac{AF}{AE}$=$\frac{1}{3}$.
∴AF=3.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的性质、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
13. 如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
 如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )| A. | 32° | B. | 53° | C. | 64° | D. | 74° |
8. 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:
(1)表中空缺的数据为9%;(精确到1%)
(2)求统计表中增长率的平均数及中位数;
(3)预测2017年的观影人次,并说明理由.
 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年增长率 | 31% | 27% | 32% | 35% | 52% |
(2)求统计表中增长率的平均数及中位数;
(3)预测2017年的观影人次,并说明理由.
 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=34度.
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=34度.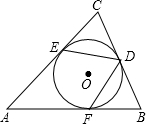 如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°. 如图,四边形ABCD的顶点均在⊙O上,⊙O的半径为2,如果∠D=45°,那么$\widehat{AC}$的长为π(结果用π表示).
如图,四边形ABCD的顶点均在⊙O上,⊙O的半径为2,如果∠D=45°,那么$\widehat{AC}$的长为π(结果用π表示). 已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).
已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).