题目内容
6.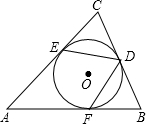 如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
分析 连接OE、OF,根据切线的性质得到∠OEA=∠OFA=90°,求出∠EOF,根据圆周角定理计算即可.
解答 解: 连接OE、OF,
连接OE、OF,
∵⊙O内切于△ABC,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°-∠A=130°,
由圆周角定理得,∠EDF=$\frac{1}{2}$∠EOF=65°,
故答案为:65°.
点评 本题考查的是三角形的内切圆和内心的概念和性质以及圆周角定理的应用,掌握切线的性质、圆周角定理是解题的关键.

练习册系列答案
相关题目
16.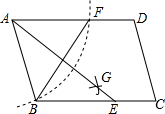 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 3$\sqrt{7}$ | D. | 4$\sqrt{7}$ |
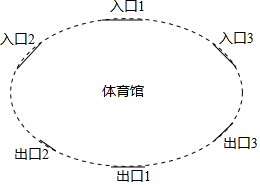 某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开
某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开
 如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.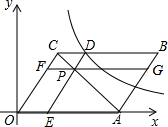 如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.
如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.