题目内容
 如图△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4cm.求:
如图△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4cm.求:(1)∠DAC的度数.
(2)BC的长.
考点:含30度角的直角三角形,等腰三角形的性质
专题:
分析:(1)由AB=AC,∠C=30°,可得∠B的度数,利用三角形内角和可求得∠BAC的度数,由AB⊥AD,即可求出∠DAC的度数;
(2)由含30度角的直角三角形及等腰三角形的性质可求得BD与DC的长度,利用BC=BD+DC即可求解.
(2)由含30度角的直角三角形及等腰三角形的性质可求得BD与DC的长度,利用BC=BD+DC即可求解.
解答:解:(1)∵AB=AC,∠C=30°,
∴∠B=30°,
∴∠BAC=180°-30°-30°=120°,
∵AB⊥AD,
∴∠DAC=120°-90°=30°,
(2)∵AD=4cm,∠B=30°,∠BAD=90°
∴BD=8cm,
∵∠DAC=30°=∠C,
∴DC=AD=4cm,
∴BC=BD+DC=12cm.
∴∠B=30°,
∴∠BAC=180°-30°-30°=120°,
∵AB⊥AD,
∴∠DAC=120°-90°=30°,
(2)∵AD=4cm,∠B=30°,∠BAD=90°
∴BD=8cm,
∵∠DAC=30°=∠C,
∴DC=AD=4cm,
∴BC=BD+DC=12cm.
点评:本题主要考查了含30度角的直角三角形及等腰三角形的性质,解题的关键是灵活运用30度角的直角三角形的性质.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,AC=AD,∠C=∠D=90°,那么△ABC与△ABD全等的理由是( )
如图,AC=AD,∠C=∠D=90°,那么△ABC与△ABD全等的理由是( )| A、HL | B、SAS |
| C、ASA | D、AAS |
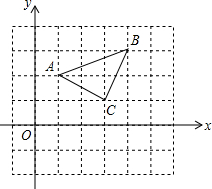 如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.
如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标. 如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为x=-1,与x轴交于点A,B(1,0),与y轴交于点C,则下列四个结论:①abc<0;②4a-2b+c>0;③2a+b=0;④当y<0时,x<-3或x>1.其中正确的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为x=-1,与x轴交于点A,B(1,0),与y轴交于点C,则下列四个结论:①abc<0;②4a-2b+c>0;③2a+b=0;④当y<0时,x<-3或x>1.其中正确的个数是( )