题目内容
7.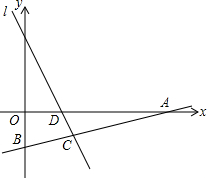 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.(1)点D的坐标为(1,0);
(2)求直线l2的表达式;
(3)求△ADC的面积;
(4)若有过点C的直线CE把△ADC的面积分为2:1两部分,请直接写出直线CE的表达式.
分析 (1)利用直线l1的解析式令y=0,求出x的值即可得到点D的坐标;
(2)根据点B、A的坐标,利用待定系数法求一次函数解析式解答;
(3)先求出点C的坐标,再求出AD的长,然后利用三角形的面积公式列式进行计算即可得解;
(4)当过点C的直线CE把△ADC的面积分为2:1两部分时,分DE:EA=2:1,或DE:EA=1:2两种情况解答即可.
解答 解:(1)把y=0代入y=-2x+2,可得:-2x+2=0,
解得:x=1,
所以点D的坐标为(1,0),
故答案为:(1,0);
(2)设l2的表达式为:y=kx+b
根据题意,得$\left\{\begin{array}{l}{0=4k+b}\\{-1=b}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=-1}\end{array}\right.$
所以l2的表达式为:y=$\frac{1}{4}$x-1;
(3)解方程组$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{1}{4}x-1}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$,
所以点C的坐标为($\frac{4}{3}$,-$\frac{2}{3}$),
过点C做CE⊥AD于点E,如图: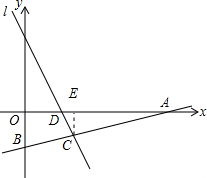
${S}_{△ADC}=\frac{1}{2}AD•CE=\frac{1}{2}×3×\frac{2}{3}=1$,
所以△ADC的面积为1;
(4)当过点C的直线CE把△ADC的面积分为2:1两部分时,可得:DE:EA=2:1,或DE:EA=1:2,
可得点E的坐标为(3,0)或(2,0)
把(3,0)和($\frac{4}{3}$,-$\frac{2}{3}$)代入解析式可得直线CE的表达式为 y=$\frac{2}{5}x-\frac{6}{5}$
把(2,0)和($\frac{4}{3}$,-$\frac{2}{3}$)代入解析式可得直线CE的表达式为y=x-2.
点评 本题考查了两直线相交的问题,直线与坐标轴的交点的求解,待定系数法求一次函数解析式,以及一次函数图象与二元一次方程组的关系,都是基础知识,一定要熟练掌握并灵活运用.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 120 | 80 |
| 乙型挖掘机 | 100 | 60 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
| A. | 4 | B. | 8 | C. | 9 | D. | -8 |
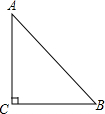 如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长. 如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=60°,则∠DAC=20°.
如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=60°,则∠DAC=20°.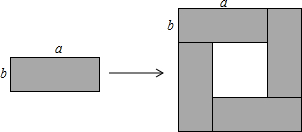
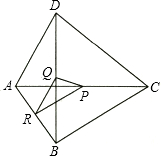 如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$. 已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.
已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.