题目内容
16.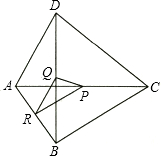 如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.(1)试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{PQ}$;(需写出必要的说理过程)
(2)画出向量$\overrightarrow{PQ}$分别在$\overrightarrow{a}$,$\overrightarrow{b}$方向上的分向量.
分析 (1)由点P、Q、R分别是对角线AC、BD和边AB的中点,直接利用三角形中位线的性质,即可求得$\overrightarrow{PR}$=$\frac{1}{2}$$\overrightarrow{CB}$=-$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{RQ}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{b}$,再利用三角形法则求解即可求得答案;
(2)利用平行线四边形法则求解即可求得答案.
解答  解:(1)∵点P、Q、R分别是对角线AC、BD和边AB的中点,
解:(1)∵点P、Q、R分别是对角线AC、BD和边AB的中点,
∴$\overrightarrow{PR}$=$\frac{1}{2}$$\overrightarrow{CB}$=-$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{RQ}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{PQ}$=$\overrightarrow{PR}$+$\overrightarrow{RQ}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$;
(2)如图:$\overrightarrow{PR}$与$\overrightarrow{PE}$即为所求.
点评 此题考查了平行向量的知识.注意掌握三角形法则与平行四边形法则的应用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.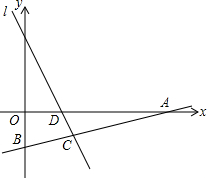 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.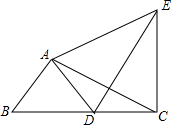 如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.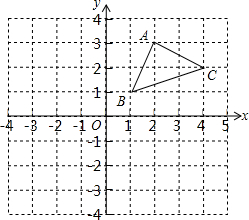 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2). 如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,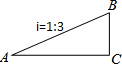 如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米.
如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米. 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: