题目内容
17.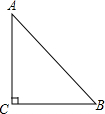 如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
分析 “有趣中线”分三种情况,两个直角边跟斜边,而直角三角形的斜边的中点到三顶点距离相等,不符合;两个直角边,有一种情况有趣中线为1.但是不符合较短的一条直角边边长为1,只能为另一条直角边上的中线,利用勾股定理求出即可.
解答 解:“有趣中线”有三种情况:
若“有趣中线”为斜边AB上的中线,直角三角形的斜边的中点到三顶点距离相等,不合题意;
若“有趣中线”为BC边上的中线,根据斜边大于直角边,矛盾,不成立;
若“有趣中线”为另一直角边AC上的中线,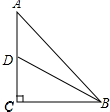 如图所示,BC=1,
如图所示,BC=1,
设BD=2x,则CD=x,
在Rt△CBD中,根据勾股定理得:BD2=BC2+CD2,即(2x)2=12+x2,
解得:x=$\frac{\sqrt{3}}{3}$,
则△ABC的“有趣中线”的长等于$\frac{2\sqrt{3}}{3}$.
点评 此题考查了勾股定理、新定义;熟练掌握新定义,由勾股定理得出方程是解本题的关键,注意分类讨论.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
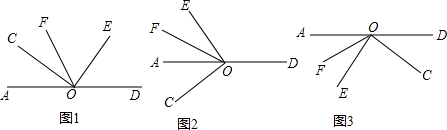
12.如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )


| A. | O→B→A→O | B. | O→A→C→O | C. | O→C→D→O | D. | O→B→D→O |
2.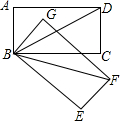 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
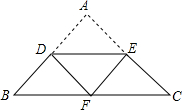 如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2. 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.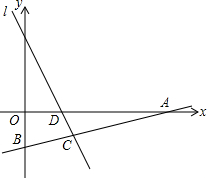 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.