题目内容
12.如图将4个长、宽分别均为a、b的长方形,摆成了一个大的正方形.利用面积的不同表示方法写出一个代数恒等式是(a+b)2-(a-b)2=4ab.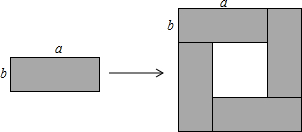
分析 通过观察可以得大正方形边长为a+b,小正方形边长为a-b,利用大正方形面积减去小正方形面积即为阴影部分面积,得出答案.
解答 解:观察图形得:
大正方形边长为:a+b,
小正方形边长为:a-b,
根据大正方形面积-小正方形面积=阴影面积得:
(a+b)2-(a-b)2=4ab.
故答案为:(a+b)2-(a-b)2=4ab.
点评 题目考查了完全平方公式的几何背景,学生需要掌握完全平方公式和几何图形的关系即可.题目整体涉及很好,可以考查学生的观察能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.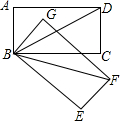 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
20.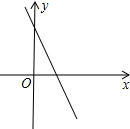 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )| A. | m>n | B. | m<n | C. | m≥n | D. | m≤n |
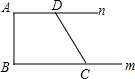 如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.
如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.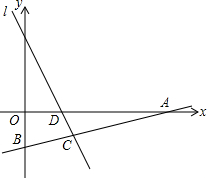 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C. 二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是-1<x<3.
二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是-1<x<3.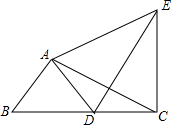 如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$. 如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0, 如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.