题目内容
16.等腰三角形的周长是36,底边长10,则顶角平分线的长是12.分析 根据题意画出图形,再由等腰三角形的性质求出腰长,根据勾股定理即可得出结论.
解答  解:如图所示,过点A作AD⊥BC于点D,
解:如图所示,过点A作AD⊥BC于点D,
∵AB=AC,BC=10,
∴AB=AC=$\frac{36-10}{2}$=13,AD平分∠BAC,
∴BD=$\frac{1}{2}$BC=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12.
故答案为:12.
点评 本题考查的是勾股定理及等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
相关题目
7.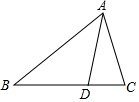 如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
 如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )
如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )| A. | a | B. | $\frac{1}{2}a$ | C. | $\frac{1}{3}a$ | D. | $\frac{1}{4}$a |
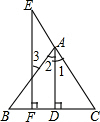 如图:已知:AD⊥BC于D,EF⊥BC于F,∠E=∠3,∠1与∠2相等吗?试说明理由.
如图:已知:AD⊥BC于D,EF⊥BC于F,∠E=∠3,∠1与∠2相等吗?试说明理由. 某校计划修建一个长方形花坛,要求花坛的长与宽的比为2:1,如图所示花坛中间为花卉种植区域,花卉种植区域前侧留有2米宽的空地,其它三侧各保留1米宽的通道,如果要求花卉种植区域的面积是55平方米,那么整个花坛的长与宽应为多少米?
某校计划修建一个长方形花坛,要求花坛的长与宽的比为2:1,如图所示花坛中间为花卉种植区域,花卉种植区域前侧留有2米宽的空地,其它三侧各保留1米宽的通道,如果要求花卉种植区域的面积是55平方米,那么整个花坛的长与宽应为多少米?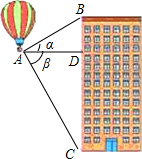 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.
如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.