题目内容
19．在Rt△ABC中，∠C=90°，AB：BC=5：3，AC=16，求AB、BC的长．分析 根据题意画出图形，设BC=3x，则AC=5x，再由勾股定理求出x的值，进而可得出结论．
解答 
解：如图，
∵在Rt△ABC中，∠C=90°，AB：BC=5：3，AC=16，
∴设BC=3x，则AC=5x．
∵AC2+BC2=AB2，即162+（3x）2=（5x）2，解得x=4，
∵AB=20，BC=12．
点评 本题考查的是勾股定理及解一元二次方程，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
10．麓山组织学生到商场参加社会实践活动，他们参与了某种品牌运动鞋的销售工作，已知该运动鞋每双的进价为100元，为寻求合适的销售价格进行了4天的试销，试销情况如表所示：
（1）观察表中数据，x，y满足什么函数关系？请求出这个函数关系式；
（2）假设售价与销售量始终满足（1）中所求函数关系，若商场计划每天的销售利润为3500元，则其单价应定为多少元？
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x（元/双） | 150 | 200 | 250 | 300 |
| 销售量y（双） | 40 | 30 | 24 | 20 |
（2）假设售价与销售量始终满足（1）中所求函数关系，若商场计划每天的销售利润为3500元，则其单价应定为多少元？
7．
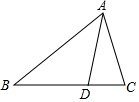如图，D是△ABC的边BC上任一点，已知AB=6，AD=3，∠DAC=∠B．若△ABD的面积为a，则△ACD的面积为（ ）
如图，D是△ABC的边BC上任一点，已知AB=6，AD=3，∠DAC=∠B．若△ABD的面积为a，则△ACD的面积为（ ）| A． | a | B． | $\frac{1}{2}a$ | C． | $\frac{1}{3}a$ | D． | $\frac{1}{4}$a |
某校计划修建一个长方形花坛，要求花坛的长与宽的比为2：1，如图所示花坛中间为花卉种植区域，花卉种植区域前侧留有2米宽的空地，其它三侧各保留1米宽的通道，如果要求花卉种植区域的面积是55平方米，那么整个花坛的长与宽应为多少米？