题目内容
5.如图.等腰直角三角形ABC中,∠A=90°,P为BC的中点,小明拿着含45°角的透明三角形,使45°角的顶点落在点P,且绕P旋转.(1)如图①:当三角板的两边分别AB、AC交于E、F点时,试说明△BPE∽△CFP.
(2)将三角板绕点P旋转到图②,三角板两边分别交BA延长线和边AC于点E,F.连接EF,△BPE与△EFP是否相似?请说明理由.
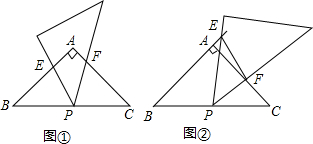
分析 (1)由∠BAC=90°,AB=AC易得∠B=∠C=45°,利用三角形的内角和定理可得∠BPE+∠EPB=135°,同理可得∠BPE+∠CPF=135°,易得∠BPE=∠CPF,又因为∠B=∠C,由AA定理易得△BPE∽△CFP;
(2)由(1)中的结论△BPE∽△CFP,利用相似三角形的性质可得$\frac{BE}{CP}=\frac{PE}{FP}$,因为BP=CP,可得$\frac{BE}{BP}=\frac{PE}{FP}$,利用SAS定理可得△BPE与△EFP相似.
解答 (1)证明:如图①,∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠EPB=135°,
∵∠EPF=45°,∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,
∴∠BPE=∠CPF,
∵∠B=∠C,
∴△BPE∽△CFP;
(2)解:△BPE与△EFP相似,
理由:如图②,
∵△BPE∽△CFP,
∴$\frac{BE}{CP}=\frac{PE}{FP}$,
∵CP=BP,
∴$\frac{BE}{BP}=\frac{PE}{FP}$,
∵∠B=∠EPF=45°,
∴△BPE∽△EFP.
点评 本题主要考查了相似三角形的性质及判定,利用三角形的内角和定理发现角的关系是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
16.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.下列运算中,正确的是( )
| A. | x3•x=x4 | B. | (-3x)2=6x2 | C. | 3x3-2x2=x | D. | x6÷x2=x3 |
17.某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
| 人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次测试成绩的众数是55分 | |
| C. | 该班学生这次测试成绩的中位数是60分 | |
| D. | 该班学生这次测试成绩的平均数是59分 |
15.下列说法正确的是( )
| A. | 袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球 | |
| B. | 天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 | |
| C. | 某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖 | |
| D. | 连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
 如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.
如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.
 已知二次函数y=x2-(2k+1)x+k2+k(k>0)
已知二次函数y=x2-(2k+1)x+k2+k(k>0)