题目内容
14.在平面直角坐标系中作△OMN,其中三个顶点分别是O(0,0),M(1,1),N(x,y)(-2≤x≤2,-2≤y≤2,x,y的值均为整数),则所作△OMN不是直角三角形的概率为( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{6}$ |
分析 根据已知得出A点坐标,进而得出△OMN为直角三角形时N点坐标个数,得出不是直角三角形时N点坐标个数,进而利用概率公式求出即可.
解答 解:∵N(x,y)(-2≤x≤2,-2≤y≤2,x,y均为整数),
∴N点坐标可以为:
(-2,-1),(-2,0),(-2,1),(-2,2),
(-1,-2),(-1,0),(-1,1),(-1,2),
(0,-2),(0,-1),(0,1),(0,2),
(1,-2),(1,-1),(1,0),(1,2),
(2,-2),(2,-1),(2,0),(2,1);
只有N点坐标为:(0,2)(0,1),(1,0),(2,0),(1,-1),(-1,1),(2,-2),(-2,2)一共8种情况时△OMN为直角三角形,
∴所作△OMN不是直角三角形的概率是$\frac{20-8}{20}$=$\frac{3}{5}$.
故选:C.
点评 此题考查了直角三角形的性质和判定以及概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.2-1等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
4.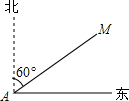 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )
 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )| A. | 50$\sqrt{3}$ | B. | 40 | C. | 30 | D. | 20 |
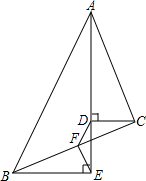 如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.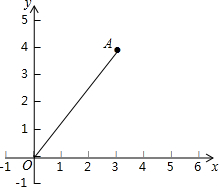 在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.
在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.