题目内容
4．
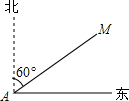如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60°方向上，且AM=100海里，那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置（ ）| A． | 50$\sqrt{3}$ | B． | 40 | C． | 30 | D． | 20 |
分析 过M作东西方向的垂线，设垂足为N，根据垂线段最短可知此时渔船离灯塔的距离最近．由题易可得∠MAN=30°，在Rt△MAN中，根据锐角三角函数的定义求出AN的长即可．
解答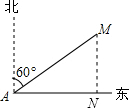 
解：如图，过M作东西方向的垂线，设垂足为N．
易知：∠MAN=90°-60°=30°．
在Rt△AMN中，∵∠ANM=90°，∠MAN=30°，AM=100海里，
∴AN=AM•cos∠MAN=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$海里．
故该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置．
故选A．
点评 本题主要考查了解直角三角形的应用-方向角问题，三角函数的定义，利用垂线段最短的性质作出辅助线是解决本题的关键．
练习册系列答案
相关题目
14．在平面直角坐标系中作△OMN，其中三个顶点分别是O（0，0），M（1，1），N（x，y）（-2≤x≤2，-2≤y≤2，x，y的值均为整数），则所作△OMN不是直角三角形的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{5}{6}$ |
9．在数轴上表示不等式3x+1≥4的解集，正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
16．下列实数中，无理数是（ ）
| A． | $\sqrt{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{π}{2}$ |