题目内容
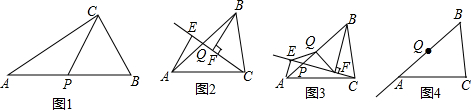
10.不能判定直线MN是线段AB的中垂线的是( )| A. | MA=MB,NA=NB | |
| B. | MA=MB,MN⊥AB | |
| C. | MA=NA,BM=BN | |
| D. | MA=MB,且点M不在线段AB上,MN平分AB |
分析 根据线段垂直平分线性质和等腰三角形的性质逐个判断即可.
解答 解:A、∵MA=MB,NA=NB,
∴M、N都在BA的垂直平分线上,
即MN是线段AB的垂直平分线,故本选项错误;
B、∵MA=MB,MN⊥AB,
∴MN平分AB,
即MN是线段AB的垂直平分线,故本选项错误;
C、∵MA=NA,MB=NB,
∴A、B都在MN的垂直平分线上,
即AB是线段MN的垂直平分线,不能推出MN是线段AB的垂直平分线,故本选项正确;
D、∵MA=MB,MN平分AB,
∴MN⊥AB,
即MN是线段AB的垂直平分线,故本选项错误;
故选C.
点评 本题考查了线段垂直平分线性质和等腰三角形的性质的应用,能熟记线段垂直平分线性质定理的内容是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
1.等边三角形的面积为8$\sqrt{3}$cm2,则它的高为( )
| A. | 2$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 2$\sqrt{6}$cm | D. | 2$\sqrt{5}$cm |
5.已知$\left\{\begin{array}{l}{2a+b=3}\\{3a-4b=10}\end{array}\right.$,则a-b等于( )
| A. | 3 | B. | $\frac{3}{4}$ | C. | 4 | D. | 1 |
15.三位同学在一起探讨问题,甲说:等腰三角形顶角的角平分线是它的对称轴;乙说:等腰三角形底边上的高或中线也是它的对称轴;丙说:你们说的都不对,底边上的中垂线才是等腰三角形的对称轴,你认为( )
| A. | 甲说的对 | B. | 乙说的对 | C. | 丙说的对 | D. | 都不对 |
2.在已知等腰三角形的前提下,再添加下列一个条件后仍不能成为等边三角形的是( )
| A. | 顶角等于60度 | B. | 两个底角平分线的夹角等于120度 | ||
| C. | 底边上的高与一腰上的高相等 | D. | 底边上的中线与一腰上的中线相等 |