题目内容
9.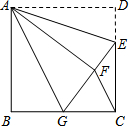 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.(1)求∠AEC+∠AGC的度数;
(2)求证:BG=GC.
分析 (1)根据正方形的性质,翻折的性质求得∠GAE=45°,根据四边形内角和为360°可得∠AEC+∠AGC=360°-∠GAE-∠BCD=225°;
(2)在直角△ECG中,根据勾股定理可证BG=GC.
解答 解:(1)在正方形ABCD中,
∵AB=BC=CD,∠BAD=∠BCD=90°,
由对折可知:∠DAE=∠FAE,∠BAG=∠FAG,
∴∠GAE=$\frac{1}{2}$∠BAD=45°,
四边形AGCE中,∠AEC+∠AGC=360°-∠GAE-∠BCD=225°;
(2)∵AB=DC=6,CE=2DE,
∴CE=4,DE=2,
设BG=FG=x,则CG=6-x.
∵DE=EF=2,
在Rt△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,
解得x=3.
∴BG=3,CG=6-3=3;
∴BG=GC.
点评 本题考查了翻折变换的性质和正方形的性质,勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
19.现有相同个数的甲、乙两组数据,经计算得:$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,且S甲2=0.35,S乙2=0.25,比较这两组数据的稳定性,下列说法正确的是( )
| A. | 甲比较稳定 | B. | 乙比较稳定 | C. | 甲、乙一样稳定 | D. | 无法确定 |
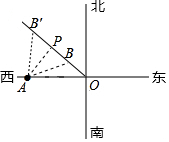 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414) 如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.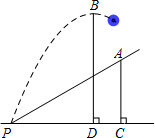 如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.