题目内容
14．已知关于x的方程x2+kx+k-3=0，求证：不论k取何实数，该方程都有两个不相等的实数根．分析 根据方程的系数结合根的判别式，即可得出△=（k-2）2+8＞0，由此即可证出：不论k取何实数，该方程都有两个不相等的实数根．
解答 证明：∵在方程x2+kx+k-3=0中，△=k2-4×1×（k-3）=k2-4k+12=（k-2）2+8＞0，
∴不论k取何实数，该方程都有两个不相等的实数根．
点评 本题考查了根的判别式，牢记“当△＞0时，方程有两个不相等的实数根”是解题的关键．
练习册系列答案
相关题目
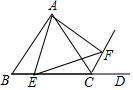如图，在等边△ABC中，AB=4，点E在BC边上，将射线AE绕点A逆时针旋转60°，与△ABC的外角∠ACD的平分线交于点F，连接AF．设BE=x，△AEF的面积为y，则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$．
5．一元二次方程x2-x-1=0和2x2-6x+5=0，这两个方程的所有实数根之和为（ ）
| A． | 4 | B． | -4 | C． | -6 | D． | 1 |
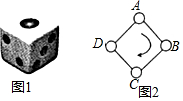如图1，一枚质地均匀的正六面体骰子的六个面分别标有数字1，2，3，4，5，6，如图2，正方形ABCD的顶点处各有一个圈，跳圈游戏的规则为：游戏者每掷一次骰子，骰子朝上的那面上的数字是几，就沿正方形的边按顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落在圈D；若第二次掷得2，就从圈D开始顺时针连续跳2个边长，落得圈B；…设游戏者从圈A起跳．
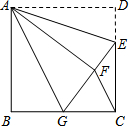如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．G为BC上的一点，将△ADE沿AE对折至△AFE，同时将△ABG沿AG对折至△AFG，连接CF．
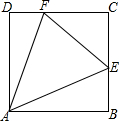如图，四边形ABCD为正方形（各边相等，各内角为直角），E是BC边上一点，F是CD上的一点．
