题目内容
1.解方程(1)2x2-4x-3=0(用配方法)
(2)3x(x-2)=2(2-x)
分析 (1)借助完全平方公式,将原方程变形为(x-1)2=$\frac{5}{2}$,开方,即可解决问题;
(2)先移项,然后通过提取公因式(x-2)对等式的左边进行因式分解,再来求x的值.
解答 解:(1)∵2x2-4x-3=0,
∴x2-2x=$\frac{3}{2}$,
∴(x-1)2=$\frac{5}{2}$,
∴x-1=±$\frac{\sqrt{10}}{2}$,
∴x1=1+$\frac{\sqrt{10}}{2}$,x2=1-$\frac{\sqrt{10}}{2}$;
(2)3x(x-2)=2(2-x),
3x(x-2)+2(x-2)=0,
(x-2)(3x+2)=0,
则x-2=0或3x+2=0,
解得x1=2,x2=-$\frac{2}{3}$.
点评 本题考查了因式分解法和配方法解方程.应该根据方程的特点选择解一元二次方程的方法.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.关于x的一元二次方程(m-3)x2+2x-1=0有实数根,则m的取值范围是( )
| A. | m≥2 | B. | m>2 | C. | m≥2且m≠3 | D. | m>2且m≠3 |
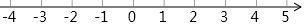 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$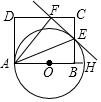 如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.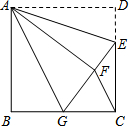 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF. 如图所示,△ABC两个外角的平分线BP、CP相交于点P.
如图所示,△ABC两个外角的平分线BP、CP相交于点P.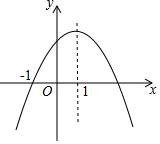 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2-4ac=0;④8a+c<0;⑤a:b:c=-1:2:3,其中正确的结论有①④⑤.
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2-4ac=0;④8a+c<0;⑤a:b:c=-1:2:3,其中正确的结论有①④⑤.