题目内容
16.已知:在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=16,BC=12,求sin∠DCA和tan∠DCA的值.分析 在直角△ABC中,根据勾股定理即可求得AB,而∠B=∠ACD,即可把求sin∠ACD转化为求sinB.
解答 解:在直角△ABC中,根据勾股定理可得:AC=AB$\sqrt{{AB}^{2}{-BC}^{2}}$=$\sqrt{1{6}^{2}-1{2}^{2}}$=4$\sqrt{7}$.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD.
∴sin∠ACD=sin∠B=$\frac{AC}{AB}$=$\frac{4\sqrt{7}}{16}$=$\frac{\sqrt{7}}{4}$,
tan∠DCA=tan∠B=$\frac{AC}{BC}$=$\frac{4\sqrt{7}}{12}$=$\frac{\sqrt{7}}{3}$.
点评 本题考查了解直角三角形中三角函数的应用,熟练掌握好边角之间的关系是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.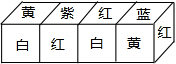 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
将四个正方体拼成一个长方体如图位置,求此时长方体的下底的花朵数之和.
 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
7.为了说明命题“当b<0时,关于x的一元二次方程x2+bx+2=0必有实数解”是假命题,可以举的一个反例是( )
| A. | b=2 | B. | b=3 | C. | b=-2 | D. | b=-3 |
1.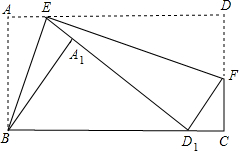 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
 已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )
已知矩形ABCD中,AB=4,AD=7,点E是边AD上的点,点F是边DC上的点,分别沿BE,EF折叠得得到点A1,D1,恰好使D1落在BC上,且E,A1,D1同线,AE>2,则AE=( )| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |