题目内容
7.为了说明命题“当b<0时,关于x的一元二次方程x2+bx+2=0必有实数解”是假命题,可以举的一个反例是( )| A. | b=2 | B. | b=3 | C. | b=-2 | D. | b=-3 |
分析 利用根的判别式结合b的值分别判断得出即可.
解答 解:A、当b=2时,此时b>0,不合题意,故此选项错误;
B、当b=3时,此时b>0,不合题意,故此选项错误;
C、当b=-2时,此时b<0,则x2-2x+2=0,故b2-4ac=4-8=-4<0,
故此方程无实数根,故此选项正确;
D、当b=-3时,此时b<0,则x2-3x+2=0,故b2-4ac=9-8=1>0,
故此方程有两个不相等的实数根,故此选项错误.
故选:C.
点评 此题主要考查了命题与定理以及根的判别式,正确记忆根的判别式与方程根的情况是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.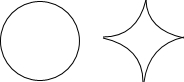 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
17.已知1米=109纳米,一个粒子的直径是35000纳米,用科学记数法表示直径为( )
| A. | 3.5×10-4米 | B. | 3.5×10-5米 | C. | 35×10-5米 | D. | 0.35×10-4米 |
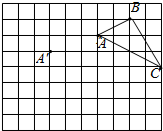 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点. 如图,△ABC中,D,E两点分别在AB,AC边上,且DE∥BC,如果$\frac{AD}{AB}=\frac{2}{3}$,AC=6,那么AE的长为( )
如图,△ABC中,D,E两点分别在AB,AC边上,且DE∥BC,如果$\frac{AD}{AB}=\frac{2}{3}$,AC=6,那么AE的长为( )