题目内容
11.在平面直角坐标系中,直线l:y=3x+b与x轴、y轴分别交于A、B两点,已知△AOB的面积为6,则直线l的函数关系式为y=3x+6或y=3x-6.分析 首先求出A、B两点的坐标分别是A(-$\frac{b}{3}$,0),B(0,b),然后根据△AOB的面积为6,求出b的值是多少,即可确定直线l的函数关系式.
解答 解:∵直线l:y=3x+b与x轴、y轴分别交于A、B两点,
∴A、B两点的坐标分别是A(-$\frac{b}{3}$,0),B(0,b),
∵△AOB的面积为6,
∴$\frac{1}{2}×{\frac{1}{3}}^{\;}$b2=6,
∴b2=36,
解得b1=6或b2=-6,
∴直线l的函数关系式为:y=3x+6或y=3x-6.
故答案为:y=3x+6或y=3x-6.
点评 此题主要考查了待定系数法求一次函数解析式,以及三角形的面积的求法,要熟练掌握,解答此题的关键是根据△AOB的面积为6,求出b的值是多少.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.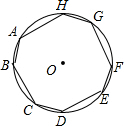 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
2.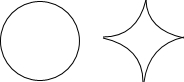 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
1.钟表的时针与分针在运行过程中每隔一定时间就相遇一次,相遇间隔的时间是( )
| A. | 1小时 | B. | $\frac{12}{11}$小时 | C. | 1.2小时 | D. | 1.1小时 |