题目内容
8．已知m是$\root{3}{31}$的整数部分，n是$\sqrt{59}$的小数部分，求m-2n的值．分析 由于3＜$\root{3}{31}$＜4，由此可得$\root{3}{31}$的整数m的值；由于7＜$\sqrt{59}$＜8，由此可得$\sqrt{59}$的小数部分n的值；进而求出m-2n的值
解答 解：∵3＜$\root{3}{31}$＜4，
∴$\root{3}{31}$的整数部分m的值为3，
∵7＜$\sqrt{59}$＜8，
∴$\sqrt{59}$的小数部分n=$\sqrt{59}$-7，
∴m-2n=3-2（$\sqrt{59}$-7）=3-2$\sqrt{59}$+14=17-2$\sqrt{59}$．
点评 本题主要考查了估算无理数的大小，注意应先判断所给的无理数的近似值然后解题．
练习册系列答案
相关题目
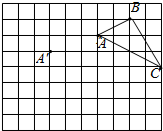在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．
17．已知1米=109纳米，一个粒子的直径是35000纳米，用科学记数法表示直径为（ ）
| A． | 3.5×10-4米 | B． | 3.5×10-5米 | C． | 35×10-5米 | D． | 0.35×10-4米 |