题目内容
14.化简求值:$\frac{2ab}{a\sqrt{b}+b\sqrt{a}}$+$\frac{a+b}{\sqrt{a}+\sqrt{b}}$,其中a=20,b=45.分析 原式分母有理化化简得到结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{2ab(a\sqrt{b}-b\sqrt{a})}{{a}^{2}b-{ab}^{2}}$+$\frac{(a+b)(\sqrt{a}-\sqrt{b})}{a-b}$
=$\frac{2a\sqrt{b}-2b\sqrt{a}+a\sqrt{a}-a\sqrt{b}+b\sqrt{a}-b\sqrt{b}}{a-b}$
=$\frac{(a-b)\sqrt{b}+(a-b)\sqrt{a}}{a-b}$
=$\sqrt{a}$+$\sqrt{b}$,
当a=20,b=45时,原式=$\sqrt{20}$+$\sqrt{45}$=2$\sqrt{5}$+3$\sqrt{5}$=5$\sqrt{5}$.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15.已知抛物线C:y=x2+3x-10,将抛物线C平移得到抛物线C′,若两条抛物线C和C′关于直线x=1对称,则下列平移方法中,正确的是( )
| A. | 将抛物线C向右平移$\frac{5}{2}$个单位 | B. | 将抛物线C向右平移3个单位 | ||
| C. | 将抛物线C向右平移5个单位 | D. | 将抛物线C向右平移6个单位 |
2.半径为R的圆内接正三角形的面积是( )
| A. | $\frac{\sqrt{3}}{2}$R2 | B. | πR2 | C. | $\frac{3\sqrt{3}}{2}$R2 | D. | $\frac{3\sqrt{3}}{4}$R2 |
6.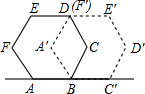 如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
 如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
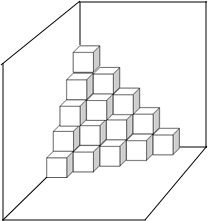 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
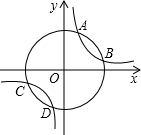 如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )