题目内容
3.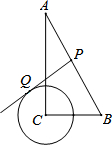 如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )
如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2-$\frac{\sqrt{3}}{3}$ |
分析 当PC⊥AB时,线段PQ最短;连接CP、CQ,根据勾股定理知PQ2=CP2-CQ2,先求出CP的长,然后由勾股定理即可求得答案.
解答 解:连接CP、CQ;如图所示: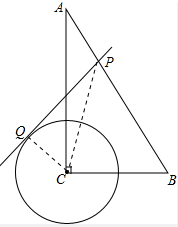
∵PQ是⊙C的切线,
∴CQ⊥PQ,∠CQP=90°,
根据勾股定理得:PQ2=CP2-CQ2,
∴当PC⊥AB时,线段PQ最短,
∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=$2\sqrt{3}$,
∴CP$\frac{AC•BC}{AB}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴PQ$\sqrt{{CP}^{2}-C{Q}^{2}}$=$\sqrt{3-1}$=$\sqrt{2}$,
∴PQ的最小值是$\sqrt{2}$,
故选C.
点评 本题考查了切线的性质以及勾股定理的运用;注意掌握辅助线的作法,注意当PC⊥AB时,线段PQ最短是关键.

练习册系列答案
相关题目
13.tan45°的值等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
11.下列运算之前的倒数( )
| A. | x4-x3=x | B. | x2x3=x6 | C. | x5÷x3=x2 | D. | (x2)3=x5 |
18.分解因式8a3-8a2+2a的结果是( )
| A. | 2a(2a-1)2 | B. | a(4a-1)2 | C. | a(2a-1)2 | D. | 2a(2a+1)2 |
15.已知抛物线C:y=x2+3x-10,将抛物线C平移得到抛物线C′,若两条抛物线C和C′关于直线x=1对称,则下列平移方法中,正确的是( )
| A. | 将抛物线C向右平移$\frac{5}{2}$个单位 | B. | 将抛物线C向右平移3个单位 | ||
| C. | 将抛物线C向右平移5个单位 | D. | 将抛物线C向右平移6个单位 |
2.半径为R的圆内接正三角形的面积是( )
| A. | $\frac{\sqrt{3}}{2}$R2 | B. | πR2 | C. | $\frac{3\sqrt{3}}{2}$R2 | D. | $\frac{3\sqrt{3}}{4}$R2 |
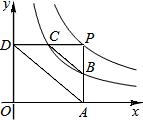 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论:
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论: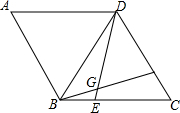 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.