题目内容
4．计算：2$\sqrt{\frac{{b}^{4}}{12a}}$．分析 根据二次根式的性质化简，即可解答．
解答 解：$2\sqrt{\frac{{b}^{4}}{12a}}=2\sqrt{\frac{{b}^{4}×3a}{12a×3a}}=2×\frac{{b}^{2}\sqrt{3a}}{6a}=\frac{{b}^{2}\sqrt{3a}}{3a}$．
点评 本题考查了二次根式的化简，解决本题的关键是熟记二次根式的性质．
练习册系列答案
相关题目
15．已知抛物线C：y=x2+3x-10，将抛物线C平移得到抛物线C′，若两条抛物线C和C′关于直线x=1对称，则下列平移方法中，正确的是（ ）
| A． | 将抛物线C向右平移$\frac{5}{2}$个单位 | B． | 将抛物线C向右平移3个单位 | ||
| C． | 将抛物线C向右平移5个单位 | D． | 将抛物线C向右平移6个单位 |
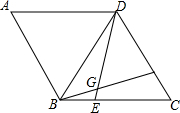在菱形ABCD中，AB=BD，点E，F分别在BC，CD上，且BE=CF，连接BF，DE交于点G．若BG=3，DG=4，则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$．
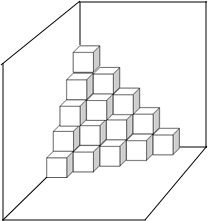如图，是按规律摆放在墙角的一些小正方体，从上往下分别记为第一层，第二层，第三层…第n层．
2．半径为R的圆内接正三角形的面积是（ ）
| A． | $\frac{\sqrt{3}}{2}$R2 | B． | πR2 | C． | $\frac{3\sqrt{3}}{2}$R2 | D． | $\frac{3\sqrt{3}}{4}$R2 |