题目内容
19.已知y+5与3x+4成正比例,且当x=1时,y=2.(1)求出y与x的函数关系式;
(2)设点P(a,-2)在上述函数图象上,求P点的坐标;
(3)如果自变量x的取值范围是0≤x≤5,求函数值y的取值范围.
分析 (1)由y+5与3x+4成正比例,设y+5=k(3x+4),将x=1,y=2代入求出k的值,确定出y与x的函数关系式;
(2)把y=-2代入即可求得;
(3)分别把x=0,x=5代入即可求得.
解答 解:(1)根据题意设y+5=k(3x+4),
将x=1,y=2代入得:2+5=7k,即k=1,
∴y+5=3x+4,
即y=3x-1;
(2)∵点P(a,-2)在函数y=3x-1图象上,
∴-2=3a-1,
∴a=-$\frac{1}{3}$
∴P(-$\frac{1}{3}$,-2);
(3)∵y=3x-1,
把x=0代入得y=-1,
把x=5代入得y=14,
∴函数值y的取值范围时-1≤y≤14.
点评 此题考查了利用待定系数法求正比例函数解析式以及正比例函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在Rt△ABC中,∠C=90°,若各边都扩大了2倍,则tanA的数值( )
| A. | 没有变化 | B. | 扩大了2倍 | C. | 缩小到$\frac{1}{2}$ | D. | 不能确定 |
9.如果$\sqrt{{(x-2)}^{2}}$=2-x,那么( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |

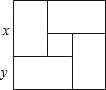 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5.
用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5. 已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将
已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将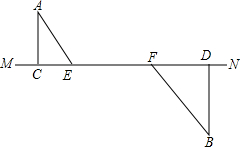 如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y.
如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y.