题目内容
19.某校九年级(2)班要举行联欢会,潇潇拿着同学们交给她的一叠正方形手工纸直发愣:为了联欢会的圆满成功,同学们需要一批圆锥形的帽子,现已知正方形手工纸的边长为40cm,若要求圆锥的侧面积最大,请你帮她完成以下问题:(1)试设计两种不同的截法(要求每一种截法尽可能减少浪费的材料),并把截法在图上表示出来;
(2)分别求出(1)中两种不同截法所得的圆锥底面的半径和高线长;
(3)若要求帽子的侧面积最大,应该选哪一种方案?
分析 (1)圆锥体的侧面展开图为扇形,然后在正方形中截出一个扇形即可;
(2)图甲:根据扇形的弧长公式求得扇形的周长,然后利用圆的周长公式可求得底面半径,最后利用勾股定理求得圆锥的高;图乙:先求得∠DFO=30°,然后可求得∠EOF=60°,接下来根据扇形的弧长公式求得扇形的周长,然后利用圆的周长公式可求得底面半径,最后利用勾股定理求得圆锥的高;
(3)依据扇形的面积公式求得扇形的面积,然后比较大小即可.
解答 解:(1)如图甲、乙所示.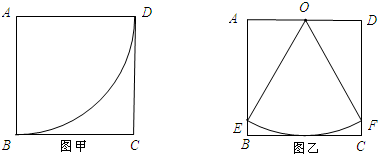
(2)方案一:如图甲:以A为圆心,AB为半径作四分之一圆,设圆锥的底面半径为r1,高为h1,则有$\frac{90}{180}π×40=2×π×{r_1}$,
解得:r1=10.
由勾股定理得:${h_1}=\sqrt{{{40}^2}-{{10}^2}}=10\sqrt{15}$;
方案二:如图乙:以AD中点0为圆心,正方形的边长为半径截取扇形QEF.
在Rt△ODF中,OD=$\frac{1}{2}$OF,所以∠DFC=30°.
∴∠DOF=∠AOE=60°.
∴∠EOF=60°.
∴L=$\frac{60×π×40}{180}=\frac{40π}{3}$.
设圆锥底面半径为r2,高为h2,则有2×π×r2=$\frac{40π}{3}$.
解得:r2=$\frac{20}{3}$.
由勾股定理得:${h_2}=\sqrt{{{40}^2}-{{(\frac{20}{3})}^2}}=\frac{20}{3}\sqrt{35}$.
∴方案一围成的圆锥底面半径为10,高为$10\sqrt{15}$;方案二围成的圆锥底面半径为$\frac{20}{3}$;高为$\frac{20}{3}\sqrt{35}$.
(3)方案一:${S}_{侧}={S}_{扇}=\frac{90×π×4{0}^{2}}{360}$=400π.
方案二:${S}_{侧}={S}_{扇}=\frac{60×π×4{0}^{2}}{360}$=$\frac{800π}{3}$.
∵400$π>\frac{800π}{3}$,
∴方案一所得的圆锥体的侧面积较大.
∴应选方案一.
点评 本题主要考查的是圆锥的计算,圆锥侧面展开图为扇形,底面圆的周长等于扇形的弧长,母线长为扇形的半径,掌握圆锥体的侧面积公式、扇形的弧长公式是解题的关键.

| A. | 两实数根之和为-1 | B. | 两实数根之积为1 | ||
| C. | 两实数根之和为1 | D. | 无实数根 |
 如图,△ABC≌△CDA,下列结论错误的是( )
如图,△ABC≌△CDA,下列结论错误的是( )| A. | ∠DAC=∠BCA | B. | ∠ADC=∠ACB | C. | ∠B=∠D | D. | AD=BC |
| A. | ±4 | B. | 4 | C. | -4 | D. | ±8 |
 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数. 如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.
如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.