题目内容
如图，△ABC中，CD⊥AB于D，若AD=2BD，AC=6，BC=| 21 |
考点：勾股定理
专题：
分析：因为CD⊥AB，所以△ACD和△BCD都是直角三角形，都利用勾股定理表示CD的长，得到方程即可求解．
解答：
解：∵CD⊥AB，
∴△ACD和△BCD都是直角三角形，
∴CD2=AC2-AD2=62-（2BD）2=36-4BD2，
CD2=BC2-BD2=（
）2-BD2=21-BD2，
∴36-4BD2=21-BD2，
解得BD2=5，
∴BD=
．
∴△ACD和△BCD都是直角三角形，
∴CD2=AC2-AD2=62-（2BD）2=36-4BD2，
CD2=BC2-BD2=（
| 21 |
∴36-4BD2=21-BD2，
解得BD2=5，
∴BD=
| 5 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
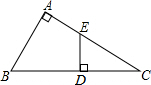如图，已知∠A=90°，AB=BD，ED⊥BC于D．求证：AE=ED．
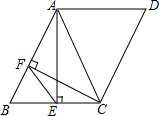已知如图，在?ABCD中，∠D=60°，AE⊥BC，CF⊥AB，垂足分别为E，F．求证：AC=2EF．
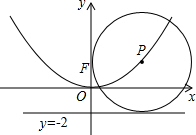如图，在平面直角坐标系xOy中，若动点P在抛物线y=ax2上，⊙P恒过点F（0，2），且与直线y=-2始终保持相切，则a=若a、b互为相反数，c、d互为倒数，|m|=2，则代数式m2-3cd+
的值为（ ）
| a+b |
| m |
| A、-1 | B、1 | C、-7 | D、1或-7 |