题目内容
11.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为120°.分析 根据O到三角形三边距离相等,得到O是内心,再利用三角形内角和定理和角平分线的概念即可求出∠BOC的度数.
解答 解:∵O到三角形三边距离相等,
∴O是内心,
∴AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=$\frac{1}{2}$∠ABC,∠BCO=∠ACO=$\frac{1}{2}$∠ACB,
∠ABC+∠ACB=180°-60°=120°,
∠OBC+∠OCB=60°,
∠BOC=180°-60°=120°.
故答案为:120°.
点评 本题考查的是角平分线的定义和三角形的内心的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
1.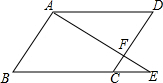 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 3:1 |
2.张明同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近一棵树的影长为8米,则这棵树的高是( )米.
| A. | 10 | B. | 6.4 | C. | 4 | D. | 无法确定 |
 如图,∠1=∠2,∠3=∠4,BC=5,则BD=5.
如图,∠1=∠2,∠3=∠4,BC=5,则BD=5. 如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.
如图,AD,AE是△ABC的∠BAC的内、外角平分线,过B作AD的垂线交AD的延长线于F,连FC并延长交AE于M,求证:AM=ME.