题目内容
1.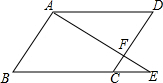 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 3:1 |
分析 根据平行四边形的性质求出△ECF∽△EDA,再根据相似三角形的性质解答即可.
解答 解:∵?ABCD边CD,
∴AD∥BC,AD=BC,
∴△ECF∽△EDA,
∴$\frac{CE}{AD}=\frac{CF}{FD}=\frac{1}{2}$,
∴$\frac{CE}{BC}=\frac{1}{2}$.
故选A.
点评 此题主要考查利用平行四边形的性质证明相似三角形,再利用相似比解题,解题的关键是熟练掌握相似三角形的性质和判定,平行四边形的性质.

练习册系列答案
相关题目
16.在Rt△ABC中,已知∠B=90°,AC=10,AB=5$\sqrt{2}$,则∠A等于( )
| A. | 45° | B. | 30° | C. | 60° | D. | 50° |
13.在直角坐标系中,与点A(2012,-1)关于x轴对称的点的坐标是( )
| A. | (2012,1) | B. | (-2012,-1) | C. | (-2012,1) | D. | (-1,2012) |
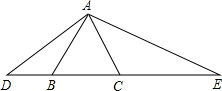 如图,△ABC是等边三角形,∠DAE=120°.求证:
如图,△ABC是等边三角形,∠DAE=120°.求证: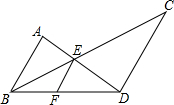 如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF.
如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF.