如图a是长方形纸带.∠DEF=21°.将纸带沿EF折叠成图b.再沿BF折叠成图c.则图c中的∠CFE的度数是( )A．117°B．119°C．138°D．159° 题目和参考答案——青夏教育精英家教网—

题目内容

2．如图a是长方形纸带，∠DEF=21°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（　　）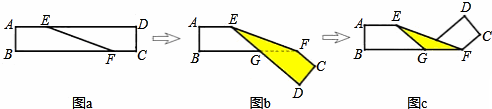

A．

117°

B．

119°

C．

138°

D．

159°

分析根据两直线平行，内错角相等可得∠EFB=∠DEF，再根据翻折的性质，图c中∠EFB处重叠了3层，然后根据根据∠CFE=180°-3∠EFB代入数据进行计算即可得解．

解答解：∵∠DEF=21°，长方形ABCD的对边AD∥BC，
∴∠EFB=∠DEF=21°，
由折叠，∠EFB处重叠了3层，
∴∠CFE=180°-3∠EFB=180°-3×21°=117°．
故选A．

点评本题考查了翻折变换，平行线的性质，观察图形判断出图c中∠EFB处重叠了3层是解题的关键．

练习册系列答案

相关题目

12．计算$\frac{1}{2}$cos30°的值为（　　）

13．

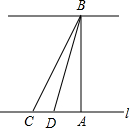某市为了改善市区交通状况，计划修建一座新大桥，如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直与新大桥AB的直线型道路l上测得如下数据：∠BDA=76.1°，∠BCA=68.2°，CD=82米．求AB的长（精确到0.1米，sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.0；sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.5．）

10．下列命题中，
（1）一个锐角的余角小于这个角；
（2）两条直线被第三条直线所截，内错角相等；
（3）a，b，c是直线，若a⊥b，b⊥c，则a⊥c；
（4）若a²+b²=0，则a，b都为0．
是假命题的有（1）（2）（3）．（请填序号）

17．下列三个命题：①平行四边形既是轴对称图形，又是中心对称图形；②平分弦的直径垂直于这条弦；
③相等圆心角所对的弧相等；④平分弧的直径垂直平分弧所对的弦．其中真命题是（　　）

7．计算：
（1）-2$\sqrt{3}$-3$\sqrt{3}$
（2）$|{-\sqrt{9}}|+\root{3}{-8}-\sqrt{\frac{1}{4}}$．

14．2016年商丘中招体育加试将跳绳作为必测项目，某中学举行“每天跳绳一分钟”活动，活动开展半年后，该校在七年级中随机抽取部分女生进行跳绳项目测试，并以测试数据为样本，绘制出如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图．

根据统计图提供的信息解答下列问题：
（1）补全频数分布直方图，并指出这个样本数据的中位数落在第三小组；
（2）若测试七年级女生“一分钟跳绳”次数不低于130次的成绩为优秀，本校九年级女生共有260人，请估计该校七年级女生“一分钟跳绳”成绩为优秀的人数；
（3）若测试七年级女生“一分钟跳绳”次数不低于170次的成绩记为满分，在这个样本中，从成绩为优秀的女生中任选一人，她的成绩为满分的概率是多少？

11．解不等式（组），并把它们的解集在数轴上表示出来．
（1）$\frac{5x+1}{6}$-2＞$\frac{x-5}{4}$
（2）$\left\{\begin{array}{l}{x-3（x-2）≥4}\\{\frac{2x-1}{5}＞\frac{x+1}{2}}\end{array}\right.$．

12．下列条件中，不能判定四边形ABCD是平行四边形的是（　　）

试题分类