题目内容
12.下列条件中,不能判定四边形ABCD是平行四边形的是( )| A. | ∠A=∠C,∠B=∠D | B. | AB∥CD,AB=CD | C. | AB∥CD,AD∥BC | D. | AB=CD,AD∥BC |
分析 根据平行四边形的判断方法一一判断即可解决问题.
解答 解:A、∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故A可以判断四边形ABCD是平行四边形.
B、∵AB∥CD,AB=CD,
∴∴四边形ABCD是平行四边形,
故B可以判断四边形ABCD是平行四边形.
C、∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
故C可以判断四边形ABCD是平行四边形.
D、∵AB=CD,AD∥BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故D不可以判断四边形ABCD是平行四边形.
故选D.
点评 本题考查平行四边形的判断、解题的关键是记住平行四边形的判定方法:两组对边分别平行的四边形是平行四边形.两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.属于中考常考题型.

练习册系列答案
相关题目
2.如图a是长方形纸带,∠DEF=21°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
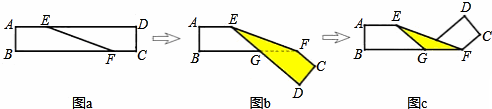

| A. | 117° | B. | 119° | C. | 138° | D. | 159° |
3.用统计图来描述某班同学的身高情况,最合适的是( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
20.正方形具有而菱形没有的性质是( )
| A. | 对角线互相垂直平分 | B. | 内角之和为360° | ||
| C. | 对角线相等 | D. | 一条对角线平分一组对角 |
4.下面能够铺满地面的正多边形的组合是( )
| A. | 正方形和正五边形 | B. | 正方形和正六边形 | ||
| C. | 正方形和正七边形 | D. | 正方形和正八边形 |
1.若关于x的不等式组$\left\{\begin{array}{l}{x-a>2}\\{x-3a<-2}\end{array}\right.$无解,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a≤2 | D. | a≥2 |
2.若点P(a,b)在第三象限,则点M(b-1,-a+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

 河堤的横断面如图1,堤高10米,迎水斜坡AB长26米,那么斜坡AB的坡度i是1:2.4.
河堤的横断面如图1,堤高10米,迎水斜坡AB长26米,那么斜坡AB的坡度i是1:2.4.