题目内容
11.解不等式(组),并把它们的解集在数轴上表示出来.(1)$\frac{5x+1}{6}$-2>$\frac{x-5}{4}$
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{2x-1}{5}>\frac{x+1}{2}}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;
(2)分别求出每一个不等式的解集,根据口诀:“同小取小”确定不等式组的解集.
解答 解:(1)去分母,得:2(5x+1)-24>3(x-5),
去括号,得:10x+2-24>3x-15,
移项,得:10x-3x>-15-2+24,
合并同类项,得:7x>7,
系数化为1,得:x>1;
将解集表示在数轴上如下:
(2)解不等式x-3(x-2)≥4,得:x≤1,
解不等式$\frac{2x-1}{5}$>$\frac{x+1}{2}$,得:x<-7,
∴不等式组的解集为:x<-7,
将解集表示在数轴上如下:
点评 本题考查的是解一元一次不等式和不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
1.下列命题中,不正确的是( )
| A. | n边形的内角和等于(n-2)•180° | |
| B. | 边长分别为3,4,5,的三角形是直角三角形 | |
| C. | 垂直于弦的直径平分弦所对的两条弧 | |
| D. | 圆的切线垂直于半径 |
2.如图a是长方形纸带,∠DEF=21°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
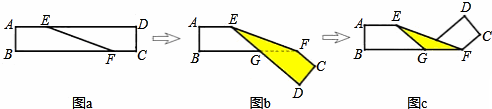

| A. | 117° | B. | 119° | C. | 138° | D. | 159° |
6.下列正多边形中,能够铺满地面的是( )
| A. | 正九边形 | B. | 正五边形 | C. | 正八边形 | D. | 正六边形 |
3.用统计图来描述某班同学的身高情况,最合适的是( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
20.正方形具有而菱形没有的性质是( )
| A. | 对角线互相垂直平分 | B. | 内角之和为360° | ||
| C. | 对角线相等 | D. | 一条对角线平分一组对角 |
