题目内容
13.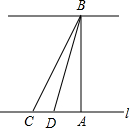 某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)
某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)
分析 设AD=x米,则AC=(x+82)米.在Rt△ABC中,根据三角函数得到AB=2.5(x+82),在Rt△ABD中,根据三角函数得到AB=4x,依此得到关于x的方程,进一步即可求解.
解答 解:设AD=x米,则AC=(x+82)米.
在Rt△ABC中,tan∠BCA=$\frac{AB}{AC}$,
∴AB=AC•tan∠BCA=2.5(x+82).
在Rt△ABD中,tan∠BDA=$\frac{AB}{AD}$,
∴AB=AD•tan∠BDA=4x.
∴2.5(x+82)=4x,
解得:x=$\frac{410}{3}$,
∴AB=4x=4×$\frac{410}{3}$≈546.7,
答:AB的长约为546.7米.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
3.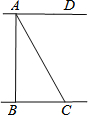 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50度,测得BC=45m,则桥长AB=( )m.| A. | $\frac{45}{cos50°}$ | B. | 45•cos50° | C. | $\frac{45}{tan50°}$ | D. | 45•tan50° |
1.下列命题中,不正确的是( )
| A. | n边形的内角和等于(n-2)•180° | |
| B. | 边长分别为3,4,5,的三角形是直角三角形 | |
| C. | 垂直于弦的直径平分弦所对的两条弧 | |
| D. | 圆的切线垂直于半径 |
8.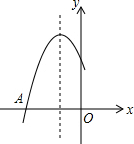 如图是二次函数y=ax2+bx+c过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac,②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )
如图是二次函数y=ax2+bx+c过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac,②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )
 如图是二次函数y=ax2+bx+c过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac,②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )
如图是二次函数y=ax2+bx+c过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac,②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
18. 小明上学期的数学成绩如表所示(单位:分)
小明上学期的数学成绩如表所示(单位:分)
(1)6次考试成绩的中位数是110,众数是110;
(2)计算小明上学期平时测试的数学平均成绩;
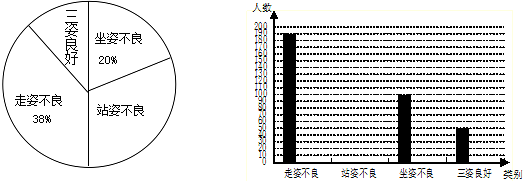
(3)如果上学期的数学总评成绩是根据如图所示的比例计算得到的,已知小明上学期的数学总评成绩为113分,那么请计算出数学总评成绩中期中、期末成绩各自所占的比例.
 小明上学期的数学成绩如表所示(单位:分)
小明上学期的数学成绩如表所示(单位:分)| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测试1 | 测试2 | 测试3 | 测试4 | |||
| 成绩 | 107 | 110 | 114 | 109 | 110 | 115 |
(2)计算小明上学期平时测试的数学平均成绩;
(3)如果上学期的数学总评成绩是根据如图所示的比例计算得到的,已知小明上学期的数学总评成绩为113分,那么请计算出数学总评成绩中期中、期末成绩各自所占的比例.
2.如图a是长方形纸带,∠DEF=21°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
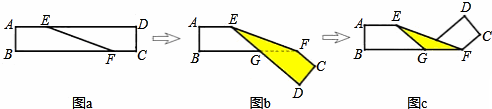

| A. | 117° | B. | 119° | C. | 138° | D. | 159° |
3.用统计图来描述某班同学的身高情况,最合适的是( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
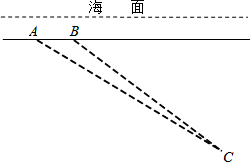 如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)
如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)